WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

ClosenessCentrality
✖
ClosenessCentrality

✖

グラフ g の頂点の接近中心性のリストを与える．

✖
ClosenessCentrality[{vw,…}]

規則 vw を使ってグラフ g を指定する．

詳細

  • ClosenessCentralityは他の頂点への平均距離が短い頂点に高い中心性を与える．
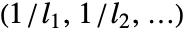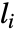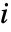  • グラフのClosenessCentralityは,として与えられる．は頂点 から 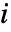に接続している他のすべての頂点への距離平均である．
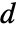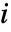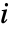  • が距離行列なら頂点 から に接続している他のすべての頂点へ平均距離 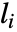は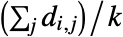 で与えられる．ただし，総和はすべての有限 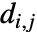の上で取られ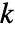， は 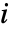に接続している頂点の数である．
  • 孤立した頂点の接近中心性は0であるとみなされる．
  • ClosenessCentralityは，無向グラフ，有向グラフ，重み付きグラフ，多重グラフ，混合グラフに用いることができる．

例題

すべて開くすべて閉じる

例  (2)基本的な使用例

接近中心性を計算する：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-dprrh4
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-3cvhh
Out[2]=2

ハイライトする：

In[3]:=3
✖
https://wolfram.com/xid/0e49egaaxvhhoe-cut8tc
Out[3]=3

頂点に順位を付ける．最も順位の高い頂点は他のすべての頂点への平均距離が短いものである：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-gtfc0a
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-8m5um
Out[2]=2

スコープ  (7)標準的な使用例のスコープの概要

ClosenessCentralityは無向グラフに使うことができる：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-ejoqzf
Out[1]=1

有向グラフ：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-d8hl64
Out[1]=1

重み付きグラフ：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-gcbs2g
Out[1]=1

多重グラフ：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-15kl6n
Out[1]=1

混合グラフ：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-czvddh
Out[1]=1

規則を使ってグラフを指定する：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-bndh30
Out[1]=1

ClosenessCentralityは大きいグラフに使うことができる：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-pq9ae
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-fgp121
Out[2]=2

アプリケーション  (9)この関数で解くことのできる問題の例

他の頂点との相対的な近さによって頂点に順位を付ける：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-occ2rm
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-kxkueu
Out[2]=2

CycleGraphの接近中心性をハイライトする：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-gzipus
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-baipzx
In[3]:=3
✖
https://wolfram.com/xid/0e49egaaxvhhoe-g2btke
In[4]:=4
✖
https://wolfram.com/xid/0e49egaaxvhhoe-h351s2
Out[4]=4

GridGraph：

In[5]:=5
✖
https://wolfram.com/xid/0e49egaaxvhhoe-jbz7i6
In[6]:=6
✖
https://wolfram.com/xid/0e49egaaxvhhoe-brg6kn
In[7]:=7
✖
https://wolfram.com/xid/0e49egaaxvhhoe-hyiutu
Out[7]=7

CompleteKaryTree：

In[8]:=8
✖
https://wolfram.com/xid/0e49egaaxvhhoe-gca8u7
In[9]:=9
✖
https://wolfram.com/xid/0e49egaaxvhhoe-gcylrp
In[10]:=10
✖
https://wolfram.com/xid/0e49egaaxvhhoe-bp9wqg
Out[10]=10

PathGraph：

In[11]:=11
✖
https://wolfram.com/xid/0e49egaaxvhhoe-zqe6n
In[12]:=12
✖
https://wolfram.com/xid/0e49egaaxvhhoe-g45cfd
In[13]:=13
✖
https://wolfram.com/xid/0e49egaaxvhhoe-j36yhw
Out[13]=13

コンピュータのアドホックネットワークはSpatialGraphDistributionを使ってモデル化することができる．感染したネットワークの中でウィルスの拡散を助けるコンピュータを求める：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-zq8ce7
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-q1ntz9

臨界コンピュータ：

In[3]:=3
✖
https://wolfram.com/xid/0e49egaaxvhhoe-ly1nz9
In[4]:=4
✖
https://wolfram.com/xid/0e49egaaxvhhoe-h07heg
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0e49egaaxvhhoe-kdp5q
Out[5]=5

イーストのタンパク質相互作用ネットワークで最も重要であると思われる10のタンパク質を求める：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-y005tc
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-dzb1t8
In[3]:=3
✖
https://wolfram.com/xid/0e49egaaxvhhoe-ebtkiz
Out[3]=3

調整ネットワークで，遺伝子間に転写調節相互作用がある場合，その遺伝子は繋がっている．グローバルな調節遺伝子である確率が最も高い遺伝子を求める：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-b3fbiu
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-frt85i
In[3]:=3
✖
https://wolfram.com/xid/0e49egaaxvhhoe-be2dey
Out[3]=3

合衆国中西部のある町における社会福祉問題に関心がある10の組織間の情報の流れを表す有向ネットワーク．他のすべての組織と最も有効に情報伝達することが可能な組織を求める：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-bx6owm
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-m2l5q0
Out[2]=2

シカゴ郊外を結ぶ道路網で，緊急車両の移動距離を最短にするのに最適な病院と消防署の位置を求める：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-dkzr47
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-lbhvyq
Out[2]=2

合衆国のWestern States Power Gridの位相を表す送電網．接近中心性が正規分布に従うことを示す：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-bfcq6b
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-fjkyg7
Out[2]//Shallow=2

正規分布を仮定して，最大尤度母数推定を求める：

In[3]:=3
✖
https://wolfram.com/xid/0e49egaaxvhhoe-hsx1l5
Out[3]=3

もとの分布と推定分布の確率密度関数を視覚的に比較する：

In[4]:=4
✖
https://wolfram.com/xid/0e49egaaxvhhoe-fjlu2x
Out[4]=4

頂点数が のグラフの場合，最も中心的な頂点と他のすべての頂点間の接近中心性の距離の差の総和はの逆数である：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-bnwnr6
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-hjjk46
Out[2]=2

最も中心の頂点がどれくらい中心であるかを他の頂点との関係で測る：

In[3]:=3
✖
https://wolfram.com/xid/0e49egaaxvhhoe-bll44s

ソーシャルネットワークの集中化：

In[4]:=4
✖
https://wolfram.com/xid/0e49egaaxvhhoe-nbbbb
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0e49egaaxvhhoe-jlsew9
Out[5]=5

特性と関係  (4)この関数の特性および他の関数との関係

ClosenessCentralityは他の接続可能な頂点への平均距離の逆である：

In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-k1hruc
In[3]:=3
✖
https://wolfram.com/xid/0e49egaaxvhhoe-kwiuen
Out[3]=3

接近可能な他の頂点との最大距離の逆：

In[4]:=4
✖
https://wolfram.com/xid/0e49egaaxvhhoe-l07hj6
In[5]:=5
✖
https://wolfram.com/xid/0e49egaaxvhhoe-f3jxv9
Out[5]=5

接近中心性は0から1までである：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-djv354
Out[1]=1

無向グラフの接近中心性は各成分の中心性に等しい：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-dxr5h8
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-945ui
Out[2]=2

各成分の中心性を計算しても同じ結果が得られる：

In[3]:=3
✖
https://wolfram.com/xid/0e49egaaxvhhoe-ch18b0
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0e49egaaxvhhoe-8dtgc
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0e49egaaxvhhoe-ikfqe4
Out[5]=5

VertexIndexを使って特定の頂点の中心性を求める：

In[1]:=1
✖
https://wolfram.com/xid/0e49egaaxvhhoe-szwpd
In[2]:=2
✖
https://wolfram.com/xid/0e49egaaxvhhoe-bbshqt
Out[2]=2
Wolfram Research (2010), ClosenessCentrality, Wolfram言語関数， https://reference.wolfram.com/language/ref/ClosenessCentrality.html （2015年に更新）.
✖
Wolfram Research (2010), ClosenessCentrality, Wolfram言語関数， https://reference.wolfram.com/language/ref/ClosenessCentrality.html （2015年に更新）.

テキスト

Wolfram Research (2010), ClosenessCentrality, Wolfram言語関数， https://reference.wolfram.com/language/ref/ClosenessCentrality.html （2015年に更新）.

✖
Wolfram Research (2010), ClosenessCentrality, Wolfram言語関数， https://reference.wolfram.com/language/ref/ClosenessCentrality.html （2015年に更新）.

CMS

Wolfram Language. 2010. "ClosenessCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/ClosenessCentrality.html.

✖
Wolfram Language. 2010. "ClosenessCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/ClosenessCentrality.html.

APA

Wolfram Language. (2010). ClosenessCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ClosenessCentrality.html

✖
Wolfram Language. (2010). ClosenessCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ClosenessCentrality.html

BibTeX

@misc{reference.wolfram_2025_closenesscentrality, author="Wolfram Research", title="{ClosenessCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/ClosenessCentrality.html}", note=[Accessed: 05-April-2025 ]}

✖
@misc{reference.wolfram_2025_closenesscentrality, author="Wolfram Research", title="{ClosenessCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/ClosenessCentrality.html}", note=[Accessed: 05-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_closenesscentrality, organization={Wolfram Research}, title={ClosenessCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/ClosenessCentrality.html}, note=[Accessed: 05-April-2025 ]}

✖
@online{reference.wolfram_2025_closenesscentrality, organization={Wolfram Research}, title={ClosenessCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/ClosenessCentrality.html}, note=[Accessed: 05-April-2025 ]}