ContinuousMarkovProcess[i0,q]
遷移率行列 q,初期状態 i0の連続時間有限状態マルコフ(Markov)過程を表す.
ContinuousMarkovProcess[p0,q]
初期状態確率ベクトル p0のマルコフ過程を表す.
ContinuousMarkovProcess[…,m,μ]
遷移行列 m,遷移率 μ のマルコフ過程を表す.
グラフ g からのマルコフ過程遷移率行列を表す.


ContinuousMarkovProcess
ContinuousMarkovProcess[i0,q]
遷移率行列 q,初期状態 i0の連続時間有限状態マルコフ(Markov)過程を表す.
ContinuousMarkovProcess[p0,q]
初期状態確率ベクトル p0のマルコフ過程を表す.
ContinuousMarkovProcess[…,m,μ]
遷移行列 m,遷移率 μ のマルコフ過程を表す.
グラフ g からのマルコフ過程遷移率行列を表す.
詳細

- ContinuousMarkovProcessは連続時間マルコフ連鎖としても知られている.
- ContinuousMarkovProcessは,連続時間・離散状態のランダム過程である.
- ContinuousMarkovProcessの状態は,1から
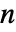 までの整数である.ただし,
までの整数である.ただし,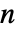 は遷移率行列 q の長さである.
は遷移率行列 q の長さである. - 無限小時間 dt について,q〚i,j〛dt は次の dt 単位の時間 q〚i,j〛dtProbability[x[t+dt]jx[t]i]において,状態 i から状態 j へ過程が遷移する確率を与える.
- 過程が遷移前に状態 i に留まる時間はExponentialDistribution[-qii]に従う.
- 遷移行列 m は条件付き遷移確率 m〚i,j〛Probability[x[tk+1]jx[tk]i]を指定する.ただし,x[tk]は時間 tkにおける状態であり,遷移率 μiは状態
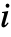 における事象間の時間がExponentialDistribution[μi]に従うように指定する.
における事象間の時間がExponentialDistribution[μi]に従うように指定する. - EstimatedProcess[data,ContinuousMarkovProcess[n]]は,n 個の状態を持つ過程を推定すべきことを示している.
- グラフ g の場合の遷移行列は,単位遷移率で各接続頂点に同等の確率で遷移するように構築される.
- ContinuousMarkovProcessでは,q は
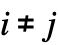 で
で 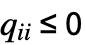 かつ
かつ 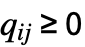 の,行の合計が0の
の,行の合計が0の 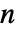 ×
×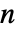 行列,i0は1から
行列,i0は1から 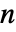 までの任意の整数,p0は合計が1になる非負の要素の長さ
までの任意の整数,p0は合計が1になる非負の要素の長さ 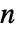 のベクトル,m は非負の要素で行の合計が1になる
のベクトル,m は非負の要素で行の合計が1になる 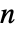 ×
× 行列,μ は正の要素の長さ
行列,μ は正の要素の長さ 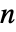 のベクトルである.
のベクトルである. - ContinuousMarkovProcessは,MarkovProcessProperties,PDF,Probability,RandomFunction等の関数で使うことができる.
予備知識
- ContinuousMarkovProcessは,連続マルコフ過程,つまり,ある与えられた状態への遷移確率が現在の状態のみに依存する,状態数が有限な連続時間過程を構築する.より厳密に言うなら,ContinuousMarkovProcessによって定義された過程は,状態数が有限であり,各状態で経過した時間が指数分布に従うような状態からなる.ContinuousMarkovProcessで定義される過程は,連続時間マルコフ連鎖(CEMC)と呼ばれることがある,時間パラメータが離散的であるDiscreteMarkovProcessによって構築された過程の連続版である.
- 連続マルコフ過程は,数学および物理科学の多くの分野に自然に見られ,待ち行列のモデル化,化学反応,電化製品の故障,地質堆積等で使われている.さらに,確率理論の見地から,連続マルコフ過程を理解するために多大な研究が行われている.
- ContinuousMarkovProcessには,数多くのパラメータスキームを使うことができる.最もよく使われるのは,ContinuousMarkovProcessが初期状態と遷移率行列
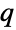 を指定する入力パラメータからCTMCを構築するものである.初期状態は,1から
を指定する入力パラメータからCTMCを構築するものである.初期状態は,1から 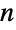 までの単一の整数
までの単一の整数 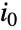 のこともあれば,和が1になる非零の要素からなる長さ
のこともあれば,和が1になる非零の要素からなる長さ 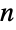 の確率ベクトル
の確率ベクトル 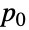 のこともある.遷移率行列
のこともある.遷移率行列 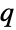 は,行の和が0で
は,行の和が0で 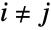 について
について 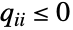 および
および 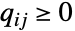 を満足する,次元が
を満足する,次元が 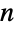 ×
×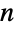 の正方行列(またはSparseArray)であり,ContinuousMarkovProcessの状態は1から
の正方行列(またはSparseArray)であり,ContinuousMarkovProcessの状態は1から 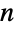 までの整数である.ContinuousMarkovProcessが状態
までの整数である.ContinuousMarkovProcessが状態 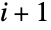 に遷移する前に状態
に遷移する前に状態 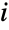 に留まる時間
に留まる時間  は,負の指数分布,すなわち tiExponentialDistribution[-qi i]に従って分布する.ただし,
は,負の指数分布,すなわち tiExponentialDistribution[-qi i]に従って分布する.ただし,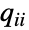 は
は 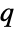 の
の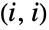 項を示し,
項を示し,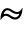 はDistributedの記号である.
はDistributedの記号である. - ContinuousMarkovProcessは,遷移行列
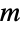 を関連する遷移率
を関連する遷移率 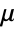 とともに使って指定することもできる.この場合,
とともに使って指定することもできる.この場合,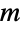 の項
の項 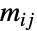 は条件付き遷移確率,つまり
は条件付き遷移確率,つまり 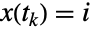 であるときの確率
であるときの確率 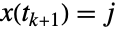 からなる.関連遷移率
からなる.関連遷移率 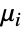 は,状態
は,状態  の事象間の時間はExponentialDistribution[μi]に従って分布するように指定する.ここで,
の事象間の時間はExponentialDistribution[μi]に従って分布するように指定する.ここで,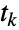 は
は 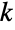 番目の状態遷移が起ったランダムな時間として定義され,
番目の状態遷移が起ったランダムな時間として定義され,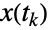 は時点
は時点 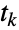 において過程が遷移する状態を示し,
において過程が遷移する状態を示し,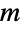 は非負の要素を持ち行の合計が1である
は非負の要素を持ち行の合計が1である  ×
×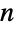 行列を,
行列を, は要素が正の長さ
は要素が正の長さ 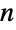 のベクトルを示す.
のベクトルを示す. - 最後に,ContinuousMarkovProcessは,頂点
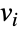 および
および 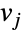 で示される事象間の遷移率を示す,辺が
で示される事象間の遷移率を示す,辺が 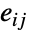 の入力グラフ
の入力グラフ 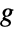 から,CTMCを作ることができる.
から,CTMCを作ることができる. - ContinuousMarkovProcessは,MarkovProcessProperties,PDF,Probabilityを含む多くの関数とともに使うことができる.RandomFunctionを使ってCTMCのシミュレーションを行うことができる.その結果(TemporalDataオブジェクト)は,ListLinePlotを使って可視化したり,TimeSeriesでスライスしたり,Mean,Variance,StandardDeviation,Moment等の関数(ContinuousMarkovProcessで定義された分布の解析にも使うことができる関数)で解析したりすることができる.ContinuousMarkovProcessは,初期状態から最終状態に最初に渡すためにCTMCに必要な時間の分布を解析するために,FirstPassageTimeDistributionの mproc パラメータとして入力することができる.一方,ContinuousMarkovProcessで構築された過程の統計的特性は,CharacteristicFunctionやCentralMomentGeneratingFunction等の関数を使って直接解析することができる.
- この統計的特性に加え,ContinuousMarkovProcessによって構築された過程は,Graphによってグラフとして表すことができ,結果としてグラフ理論の機能性を継承する.QueueingProcess,QueueProperties,SurvivalFunction等の関数は,モデリングや応用にCTMCの特性を利用する.ContinuousMarkovProcessは,指定されたデータ集合に最もよくフィットする
 状態の近似CTMCを計算する関数であるEstimatedProcessによって近似ツールとしても使うことができる.
状態の近似CTMCを計算する関数であるEstimatedProcessによって近似ツールとしても使うことができる.
例題
すべて開く すべて閉じるアプリケーション (9)
ある病院には2つの等しく互いに独立した発電装置がある.各装置が故障するまでの時間は母数 ![]() で指数関数的である.故障した発電装置を修理するのにかかる時間は,母数
で指数関数的である.故障した発電装置を修理するのにかかる時間は,母数 ![]() で指数関数的である.時間
で指数関数的である.時間 ![]() で両方の発電装置が使用可能であると仮定して,時間
で両方の発電装置が使用可能であると仮定して,時間 ![]() に両方の発電装置がまだ使用可能である確率を求める.使用可能な発電機の数は,1に使用可能な発電装置の数を加えた状態数の連続マルコフ連鎖でモデル化することができる:
に両方の発電装置がまだ使用可能である確率を求める.使用可能な発電機の数は,1に使用可能な発電装置の数を加えた状態数の連続マルコフ連鎖でモデル化することができる:
ガソリンスタンドの特殊タンクに可燃性の製品が保存されている.この製品を求める顧客が割合 ![]() のポアソン過程に従って来店する.各顧客はこの製品を1単位分求める.タンクが空のときの需要は失われる.タンクへの補給機会は割合
のポアソン過程に従って来店する.各顧客はこの製品を1単位分求める.タンクが空のときの需要は失われる.タンクへの補給機会は割合 ![]() のポアソン過程に従って訪れる.2つのポアソン過程は互いに独立であると仮定される.安全性の観点から,タンクが空にならないと補給は行われない.タンクが空になると
のポアソン過程に従って訪れる.2つのポアソン過程は互いに独立であると仮定される.安全性の観点から,タンクが空にならないと補給は行われない.タンクが空になると ![]() 単位が補給される:
単位が補給される:
ルーターは複数のユーザからパケットを受け取り,1本の送電線からこれを送信する.パケットが4ミリ秒に1つの割合でポアソン過程に従って届き,パケットの送電時間は平均3ミリ秒の指数分布に従うと仮定して,無限ルーターの容量を近似する:
ルーターの中で送電されるのを待っているパケットが6つ以上である確率を求める:
磨かれた鏡面上の傷の数はポアソン確率変数である.面積が![]() の鏡の場合,傷がない確率は0.91である.同じ過程で作成された面積が
の鏡の場合,傷がない確率は0.91である.同じ過程で作成された面積が![]() の別の鏡の鏡面に傷がない確率を求める:
の別の鏡の鏡面に傷がない確率を求める:
オイル交換所に来る車の数は,1時間に4台のポアソン過程に従う.対応する職工は1人で,オイル交換にかかる時間は指数分布に従い平均12分である.無制限の駐車場を近似する:
ある国では,自動車が路上での運転に適しているかどうかを判定するために,年に一度の検査が義務付けられている.ある自動車検査場では,運転者は車の路上適性検査が始まるまでに平均15分間待つ.検査には平均20分かかる.検査の結果,80%の車は適性検査に合格し,運転者は車で帰ることができる.15%の車は「軽欠陥」と判断される.こう判断されると,車で帰る前に平均30分の整備が必要になる.残りの5%は「重欠陥」と判断される.こう判断された車は,平均3時間の整備時間が必要になる.状態W(検査までの待ち時間),A(検査中),M(軽故障の整備),S(重故障の整備),H(帰宅)とし,連続時間マルコフモデルを使って自動車検査場の操業状態をモデル化する:
顧客が到着してから次の顧客が到着するまでの時間とサービス時間が,指数関数的である系を考える.従業員1人で2人の顧客を受け入れるスペースがある.顧客は1人が応対されている間もう1人は待っている.時点 ![]() における室内の顧客数を
における室内の顧客数を ![]() とする.これはM/M/1/2待ち行列であり,状態に
とする.これはM/M/1/2待ち行列であり,状態に ![]() として指標が付けられる次の遷移率行列を持つ出生死滅過程を使ってモデル化することができる:
として指標が付けられる次の遷移率行列を持つ出生死滅過程を使ってモデル化することができる:
これは,QueueingProcessの定常分布と一致する:
これはQueuePropertiesからの結果に一致する:
ハッブル宇宙望遠鏡には6台のジャイロスコープが搭載されている.完全な確度を得るためには,そのうち少なくとも3台が必要である.ジャイロスコープの運行時間は,独立で故障率 ![]() で指数分布に従う.4番目のジャイロスコープが故障すると,望遠鏡はスリープモードになる.こうなると以降の観測が一時中止となる.望遠鏡をスリープモードにするためには平均1/
で指数分布に従う.4番目のジャイロスコープが故障すると,望遠鏡はスリープモードになる.こうなると以降の観測が一時中止となる.望遠鏡をスリープモードにするためには平均1/![]() の指数時間が必要である.その後,地球上の基地局がスリープ信号を受け,シャトルのミッションが準備される.望遠鏡に修理クルーが到着しジャイロスコープの安定ユニットを修理するまでに平均1/
の指数時間が必要である.その後,地球上の基地局がスリープ信号を受け,シャトルのミッションが準備される.望遠鏡に修理クルーが到着しジャイロスコープの安定ユニットを修理するまでに平均1/![]() の指数時間がかかる.その間に残りの2台のジャイロスコープが故障することもある.最後のジャイロスコープが故障すると,望遠鏡がクラッシュする.
の指数時間がかかる.その間に残りの2台のジャイロスコープが故障することもある.最後のジャイロスコープが故障すると,望遠鏡がクラッシュする.![]() ,
,![]() ,
,![]() (単位は年の逆数)と仮定する:
(単位は年の逆数)と仮定する:
関連するガイド
-
▪
- 有限マルコフ(Markov)過程 ▪
- 確率過程 ▪
- 待ち行列過程
テキスト
Wolfram Research (2012), ContinuousMarkovProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html (2014年に更新).
CMS
Wolfram Language. 2012. "ContinuousMarkovProcess." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html.
APA
Wolfram Language. (2012). ContinuousMarkovProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html
BibTeX
@misc{reference.wolfram_2025_continuousmarkovprocess, author="Wolfram Research", title="{ContinuousMarkovProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_continuousmarkovprocess, organization={Wolfram Research}, title={ContinuousMarkovProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html}, note=[Accessed: 07-February-2026]}