ContinuousMarkovProcess[i0,q]
表示连续时间有限状态的马尔可夫过程,其中转移率矩阵为 q,初始状态为 i0.
ContinuousMarkovProcess[p0,q]
表示初始状态概率向量为 p0 的马尔可夫过程.
ContinuousMarkovProcess[…,m,μ]
表示转移矩阵为 m、转移率为 μ 的马尔可夫过程.
表示图 g 的马尔可夫过程转移率矩阵.


ContinuousMarkovProcess
ContinuousMarkovProcess[i0,q]
表示连续时间有限状态的马尔可夫过程,其中转移率矩阵为 q,初始状态为 i0.
ContinuousMarkovProcess[p0,q]
表示初始状态概率向量为 p0 的马尔可夫过程.
ContinuousMarkovProcess[…,m,μ]
表示转移矩阵为 m、转移率为 μ 的马尔可夫过程.
表示图 g 的马尔可夫过程转移率矩阵.
更多信息

- ContinuousMarkovProcess 也被称为连续时间马尔可夫链.
- ContinuousMarkovProcess 是连续时间离散状态的随机过程.
- ContinuousMarkovProcess 的状态是位于1和
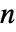 之间的整数,其中
之间的整数,其中 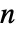 是转移率矩阵 q 的长度.
是转移率矩阵 q 的长度. - 对于无限小的时间 dt,q〚i,j〛dt 给出过程转移在下一个 dt 时间单位从状态 i 到 j 的概率q〚i,j〛dtProbability[x[t+dt]jx[t]i].
- 过程转移前在状态 i 停留的时间服从 ExponentialDistribution[-qii].
- 转移矩阵 m 指定条件转移概率 m〚i,j〛Probability[x[tk+1]jx[tk]i],其中 x[tk] 是在时刻 tk 的状态,转移率 μi 指定在状态
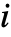 的时间之间的时间服从ExponentialDistribution[μi].
的时间之间的时间服从ExponentialDistribution[μi]. - EstimatedProcess[data,ContinuousMarkovProcess[n]] 表明具有 n 个状态的过程应该被估计.
- 在图 g 的情况下,构建具有单位转移率的转移矩阵,以给出转移至各事件顶点相等概率.
- ContinuousMarkovProcess 允许 q 为
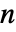 ×
×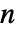 矩阵,其中对于
矩阵,其中对于 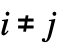 ,有
,有 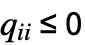 ,
,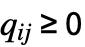 ,且各行之和为0,i0 可以是位于1 到
,且各行之和为0,i0 可以是位于1 到 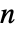 之间的整数,p0 为长为
之间的整数,p0 为长为 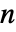 的向量,元素为非负数且和为1,m 是一个元素为非负数、各行之和为1的
的向量,元素为非负数且和为1,m 是一个元素为非负数、各行之和为1的 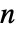 ×
×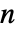 矩阵,μ 是一个由正数元素组成的长为
矩阵,μ 是一个由正数元素组成的长为 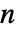 的向量.
的向量. - ContinuousMarkovProcess 可以与诸如 MarkovProcessProperties、PDF、Probability 和 RandomFunction 等函数一起使用.
背景
- ContinuousMarkovProcess 创建了一个连续马尔可夫过程,即有限状态连续时间的随机过程,其给定状态的转移概率只依赖于当前状态. 更确切的说,由 ContinuousMarkovProcess 定义的随机过程由有限多个状态组成且每个状态上的时间具备指数分布. 由 ContinuousMarkovProcess 定义的过程有时又被称为连续时间马尔可夫链(CTMC),它和由 DiscreteMarkovProcess 创建的,有离散时间参数的过程类似,只不过时间是连续的.
- 连续马尔可夫过程自然的出现在数学和物理科学的许多领域中,且被用于对队列、化学反应、电子故障和地质沉降这些现象建模. 此外,有大量的研究是关于从概率论角度理解连续马尔可夫过程的.
- ContinuousMarkovProcess 可以接受许多种参数方案. 最典型的是 ContinuousMarkovProcess 可根据指定了初始状态和转移率矩阵
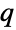 的输入参数创建 CTMC. 初始状态可能是 1 到
的输入参数创建 CTMC. 初始状态可能是 1 到 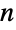 之间的单个整数
之间的单个整数 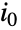 或者是长度为
或者是长度为 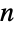 且总和为 1 的非负元素组成的概率向量. 转移率矩阵
且总和为 1 的非负元素组成的概率向量. 转移率矩阵 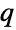 是大小为
是大小为 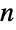 ×
×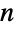 的方阵(或 SparseArray),它每行的和都是 0 且对
的方阵(或 SparseArray),它每行的和都是 0 且对 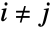 满足
满足 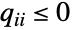 且
且 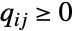 ,而 ContinuousMarkovProcess 的状态是 1 和
,而 ContinuousMarkovProcess 的状态是 1 和 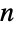 之间的整数. 对给定的 ContinuousMarkovProcess 在转移到状态
之间的整数. 对给定的 ContinuousMarkovProcess 在转移到状态 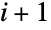 之前处于状态
之前处于状态 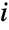 的时间
的时间 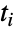 服从一个指数分布,即 tiExponentialDistribution[-qi i],其中
服从一个指数分布,即 tiExponentialDistribution[-qi i],其中 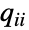 指的是矩阵
指的是矩阵 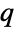 的第
的第 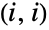 项而
项而 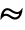 是 Distributed 的缩写.
是 Distributed 的缩写. - ContinuousMarkovProcess 也可以用一个转移矩阵
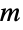 和相关的转移率
和相关的转移率 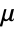 指定. 在这种情况下
指定. 在这种情况下 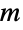 的项
的项 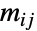 由条件转移概率组成,即给定
由条件转移概率组成,即给定 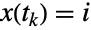 后
后 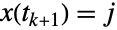 的概率,而相关的转移率
的概率,而相关的转移率 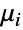 指定了状态
指定了状态 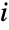 上事件间的时间分布是 ExponentialDistribution[μi]. 这里
上事件间的时间分布是 ExponentialDistribution[μi]. 这里 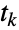 被定义成第
被定义成第 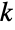
 次状态转移发生时的随机时刻,
次状态转移发生时的随机时刻,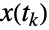 表示在时刻
表示在时刻 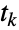 过程中的状态转移,
过程中的状态转移,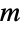 是一个
是一个 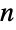 ×
×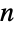 的非负元素矩阵且每行之和都是 1,而
的非负元素矩阵且每行之和都是 1,而 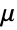 是一个长度为
是一个长度为 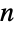 且元素为正值的向量.
且元素为正值的向量. - 最后,ContinuousMarkovProcess 可以从输入的图
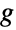 产生 CTMC,图的边
产生 CTMC,图的边 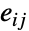 表示的是由顶点
表示的是由顶点 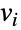 和
和 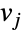 代表的事件之间的转移率.
代表的事件之间的转移率. - 许多函数都可以和 ContinuousMarkovProcess 一起使用,包括 MarkovProcessProperties、PDF 及 Probability. RandomFunction 可被用于模拟 CTMC,其结果(一个 TemporalData 对象)之后可通过 ListLinePlot 可视化,可通过 TimeSeries 切分,还可用像 Mean、Variance、StandardDeviation 和 Moment 这样的函数分析——这些函数也可用于分析由 ContinuousMarkovProcess 定义的分布. ContinuousMarkovProcess 也可作为 FirstPassageTimeDistribution 的 mproc 参数输入,来分析一个 CTMC 从初始状态第一次到达最终状态所需时间的分布,而由 ContinuousMarkovProcess 创建的随机分布的统计性质可直接用诸如 CharacteristicFunction 和 CentralMomentGeneratingFunction 这样的函数来分析.
- 除了统计性质之外,由 ContinuousMarkovProcess 创建的过程可以通过 Graph 表示为图,这样就可以继承许多图论函数的用法. 像 QueueingProcess、QueueProperties 和 SurvivalFunction 这样的函数在建模和应用中利用了 CTMC 的性质. ContinuousMarkovProcess 也可通过 EstimatedProcess 作为近似工具使用,后者是一个可以用最适合给定数据集的
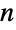 个状态计算近似 CTMC 的函数.
个状态计算近似 CTMC 的函数.
范例
打开所有单元 关闭所有单元范围 (12)
应用 (9)
一家医院拥有两个相同且独立的发电机. 每个发电机的无故障运行时间服从参数为 ![]() 的指数分布,故障发电机的维修时间服从参数为
的指数分布,故障发电机的维修时间服从参数为 ![]() 的指数分布. 假设两个发电机在
的指数分布. 假设两个发电机在 ![]() 正常运行,求两个发电机在时刻
正常运行,求两个发电机在时刻 ![]() 仍正常运行的概率. 正常运行的发电机个数可以用连续马尔可夫链模拟,其中状态数表示1加上正常运行的发电机个数:
仍正常运行的概率. 正常运行的发电机个数可以用连续马尔可夫链模拟,其中状态数表示1加上正常运行的发电机个数:
一种易燃品被存储在填充站的特殊储罐中. 需要这种产品的客户的到达服从速率为 ![]() 的泊松过程. 每个客户需要一个单位的该产品. 发生缺货的任何需求都将丢失. 重新补充库存的机会服从参数为
的泊松过程. 每个客户需要一个单位的该产品. 发生缺货的任何需求都将丢失. 重新补充库存的机会服从参数为 ![]() 的泊松过程. 假定这两个泊松过程是相互独立的. 为安全起见,只能当储罐全空时补充库存. 在这些机会发生时,补充库存
的泊松过程. 假定这两个泊松过程是相互独立的. 为安全起见,只能当储罐全空时补充库存. 在这些机会发生时,补充库存 ![]() 个单位:
个单位:
一个路由器接收来自一组用户的数据包,并将它们通过一条单一传输线传输. 假设数据包的到达是根据速率为每4毫秒一个数据包的泊松过程,数据包的传输时间为均值为3毫秒的指数分布. 求一个无限路由器的容量近似:
在一个抛光镜面表面出现缺陷的数目是一个泊松随机变量. 对于面积为 ![]() 的一面镜子,没有缺陷的概率是0.91. 求面积为
的一面镜子,没有缺陷的概率是0.91. 求面积为 ![]() 、使用相同工艺制造的另一面镜子表面没有任何瑕疵的概率:
、使用相同工艺制造的另一面镜子表面没有任何瑕疵的概率:
车抵达换油中心的模式服从泊松过程,抵达率为4辆/小时. 只有一名可用机械师,换油所花费的时间服从指数分布,平均需要12分钟. 近似无限的汽车空间:
在某一个国家,车辆每年都需要进行评估,以鉴定是否适宜在道路上行驶. 在一个车辆评估中心,司机平均需要等候15分钟,才能开始对他们的车辆是否适宜在道路上行驶进行评估. 评估需要平均20分钟就可以完成. 在评估结束之后,80%的汽车可以通过评估,允许司机把车开回家. 另外15%的车辆被归类为“轻度失败”,这些车需要平均30分钟的维修,然后司机可以把车开回家. 其余5%的车辆被归类为“重大失败”,需要对这些车辆进行平均3个小时的维修,然后才能把车开回家. 使用连续时间马尔可夫模型对车辆评估中心的运作进行建模,其中状态 W(等待评估),A(评估进行),M(轻度维修),S(重度维修)和 H(回家):
将对角线元素设置为非对角线元素的总和的相反数,使各行总和为零:
考虑一个指数型时间间隔和服务时间的系统. 为两个客户提供一台服务器和房间:一个正在服务期间,另一个正在等待. 令在时刻 ![]() ,房间中的客户数目为
,房间中的客户数目为 ![]() . 这是一个M/M/1/2的队列模型;将它作为一个生死过程,用以下的转换率矩阵进行建模,其中状态编号为
. 这是一个M/M/1/2的队列模型;将它作为一个生死过程,用以下的转换率矩阵进行建模,其中状态编号为 ![]() :
:
这与 QueueingProcess 的稳态分布相一致:
这与 QueueProperties 的结果一致:
哈勃太空望远镜携带6个陀螺仪,要求至少有三个以达到完全准确度. 陀螺仪的运行时间是独立的指数分布,故障率为 ![]() . 如果第四个陀螺仪出现故障,望远镜将进入睡眠模式,在这种模式下将暂停进一步观察. 它需要一个均值为 1/
. 如果第四个陀螺仪出现故障,望远镜将进入睡眠模式,在这种模式下将暂停进一步观察. 它需要一个均值为 1/![]() 的指数时间分布以进入睡眠模式. 在此之后,在地球上的基地台接收睡眠信号,将准备执行航天飞机飞行任务. 维修人员到达望远镜,并维修陀螺仪稳定的稳定单元,需要一个均值为1/
的指数时间分布以进入睡眠模式. 在此之后,在地球上的基地台接收睡眠信号,将准备执行航天飞机飞行任务. 维修人员到达望远镜,并维修陀螺仪稳定的稳定单元,需要一个均值为1/![]() 的指数时间. 同时,其他两个陀螺仪可能会出现故障. 如果最后一个陀螺仪出现故障,该望远镜将崩溃. 假设
的指数时间. 同时,其他两个陀螺仪可能会出现故障. 如果最后一个陀螺仪出现故障,该望远镜将崩溃. 假设 ![]() ,
,![]() ,以及
,以及 ![]() ,并全部以年的倒数为单位:
,并全部以年的倒数为单位:
文本
Wolfram Research (2012),ContinuousMarkovProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html (更新于 2014 年).
CMS
Wolfram 语言. 2012. "ContinuousMarkovProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html.
APA
Wolfram 语言. (2012). ContinuousMarkovProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html 年
BibTeX
@misc{reference.wolfram_2025_continuousmarkovprocess, author="Wolfram Research", title="{ContinuousMarkovProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html}", note=[Accessed: 07-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_continuousmarkovprocess, organization={Wolfram Research}, title={ContinuousMarkovProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/ContinuousMarkovProcess.html}, note=[Accessed: 07-December-2025]}