Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Covariance

Covariance[v,w]

gives the covariance between the vectors v and w.

Covariance[a,b]

gives the cross-covariance matrix for the matrices a and b.

gives the auto-covariance matrix for observations in matrix a.

Covariance[dist]

gives the auto-covariance matrix for the multivariate symbolic distribution dist.

Covariance[dist,i,j]

gives the (i,j) covariance for the multivariate symbolic distribution dist.

Details

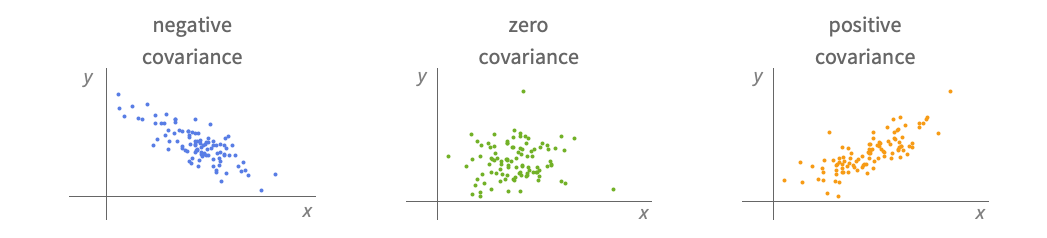
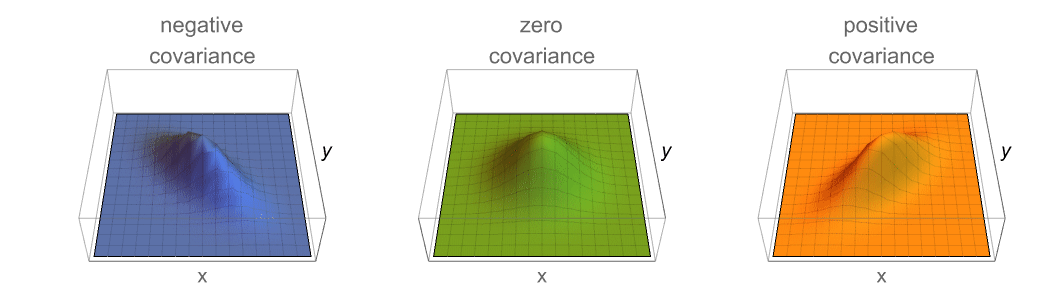
Covariance is typically used to measure covariation, i.e. whether one variable tends to vary similarly to another.
Covariance[v,w] gives the unbiased estimate of the covariance 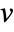between v and w.
For vectors 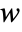and 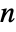of length 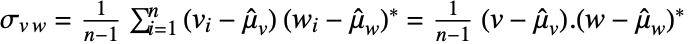, the covariance estimate Covariance[v,w] is given by 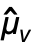with =Mean[v].

For matrices 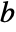and 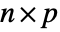with dimensions 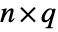and 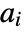and columns indexed as 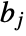and 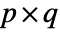, respectively, Covariance[a,b] is a 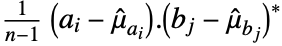matrix with elements given by :

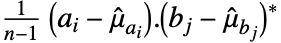where 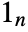is an 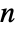-vector of ones, 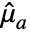is Mean[a] and 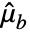is Mean[b].
For a matrix a with 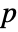columns, Covariance[a] is a 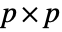matrix given by Covariance[a, a].
Covariance works with any vector that is VectorQ or matrix that is MatrixQ.
Covariance[dist,i,j] gives Expectation[(x_i-μ_i)(x_j-μ_j),{x₁,x₂,…}∈dist], where μ_i is the i 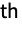component of the mean of dist. »

Covariance[dist] gives a covariance matrix with the (i,j) 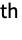entry given by Covariance[dist,i,j]. »

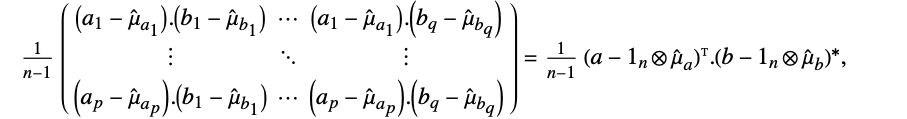
Examples

open allclose all

Basic Examples (3)

Covariance between two vectors:

Covariance matrix for a matrix:

Covariance matrix for two matrices:

Scope (13)

Data (8)

Exact input yields exact output:

Approximate input yields approximate output:

Covariance between vectors of complexes:

Works with large arrays:

A structured array can be used (see the guide):

Find the covariance for data involving quantities:

Covariance between lists of dates:

Covariance between matrices of times:

Distributions and Processes (5)

Covariance for a continuous multivariate distribution:

Covariance for a discrete multivariate distribution:

Covariance for derived distributions:

Data distribution:

Covariance matrix for a random process at times s and t:

Covariance matrix for TemporalData at times and :

Compare to the covariance of the process slice:

Applications (3)

Compute the covariance of two financial time series:

Covariance can be used to measure linear association:

Covariance can only detect monotonic relationships:

HoeffdingD can be used to detect a variety of dependence structures:

Properties & Relations (9)

The covariance matrix is symmetric and positive semidefinite:

A covariance matrix scaled by standard deviations is a correlation matrix:

Covariance and AbsoluteCorrelation are the same for a distribution with zero mean:

SpearmanRho is related to Covariance applied to ranks:

CovarianceFunction for a process is the off-diagonal entry in the covariance matrix:

Covariance and Correlation are the same for standardized vectors:

The covariance of a list with itself is the variance:

The diagonal of a covariance matrix is the variance:

The covariance tends to be large only on the diagonal of a random matrix:

Neat Examples (1)

Compute the covariance for a GCD array:

Top