Covariance
Covariance[v,w]
ベクトル v と w の間の共分散を与える.
Covariance[a,b]
行列 a と b の相互今日分散行列を与える.
Covariance[a]
行列 a の観測値についての自己共分散行列を与える.
Covariance[dist]
多変量記号分布 dist の自己共分散行列を与える.
Covariance[dist,i,j]
多変量記号分布 dist の(i,j)次共分散を与える.
詳細


- Covarianceは,しばしば,共変動,つまり,一つの変数が他の変数と同様に変化する傾向があるかどうかの測定に使われる.
- Covariance[v,w]は v と w の間の共分散
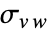 の不偏推定値を返す.
の不偏推定値を返す. - 長さが
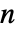 のベクトル
のベクトル 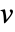 とベクトル
とベクトル 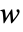 について,共分散推定Covariance[v,w]は
について,共分散推定Covariance[v,w]は 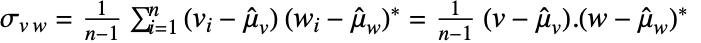 で与えられる.ただし
で与えられる.ただし 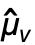 =Mean[v]である.
=Mean[v]である. - 次元がそれぞれ
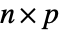 と
と 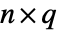 で列には
で列には 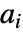 および
および 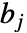 でインデックスが付けらた行列
でインデックスが付けらた行列 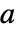 と行列
と行列 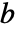 について,Covariance[a,b]は成分が
について,Covariance[a,b]は成分が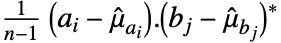 で与えられる
で与えられる 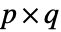 行列である.
行列である. - ただし,
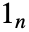 は1の
は1の 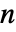 ベクトル,
ベクトル,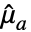 はMean[a],
はMean[a],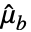 はMean[b]である.
はMean[b]である. 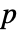 列の行列 a について,Covariance[a]はCovariance[a, a]で与えられる
列の行列 a について,Covariance[a]はCovariance[a, a]で与えられる 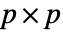 行列である.
行列である.- Covarianceは,VectorQである任意のベクトルあるいはMatrixQである任意の行列に使うことができる.
- Covariance[dist,i,j]はExpectation[(xi-μi)(xj-μj),{x1,x2,…}∈dist]を与える.ただし,μiは dist.の平均の i
 番目の成分である. »
番目の成分である. » - Covariance[dist]は(i,j)
 番目の成分がCovariance[dist,i,j]で与えられる共分散行列を与える.
番目の成分がCovariance[dist,i,j]で与えられる共分散行列を与える.
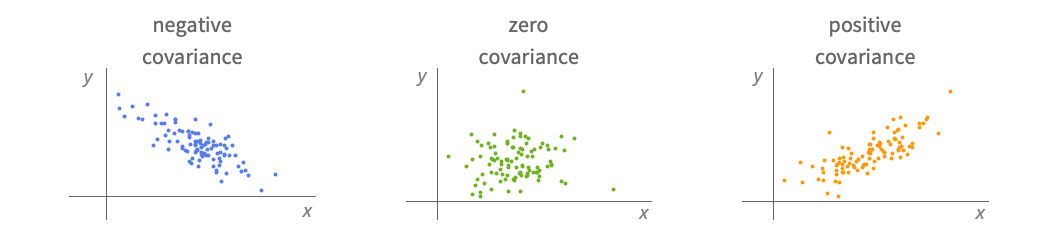
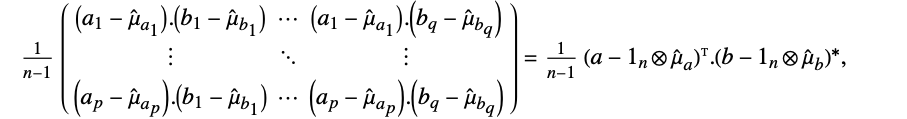
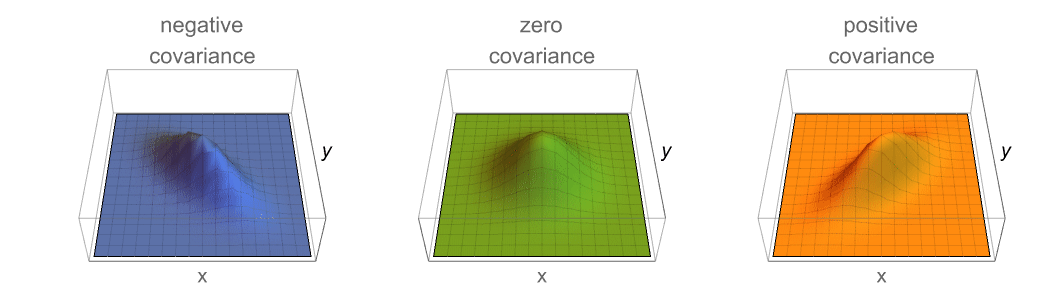
例題
すべて開くすべて閉じるスコープ (13)
データ (8)
構造化配列を使うことができる(ガイドを参照のこと):
分布と過程 (5)
時点![]() および
および![]() におけるTemporalDataについての共分散行列:
におけるTemporalDataについての共分散行列:
アプリケーション (3)
特性と関係 (9)
CovarianceおよびAbsoluteCorrelationは,ゼロ平均の分布について等しい:
SpearmanRhoは順位に適用されたCovarianceに関連する:
過程についてのCovarianceFunctionは,共分散行列の非対角項である:
CovarianceおよびCorrelationは,標準化されたベクトルについては等しい:
テキスト
Wolfram Research (2007), Covariance, Wolfram言語関数, https://reference.wolfram.com/language/ref/Covariance.html (2024年に更新).
CMS
Wolfram Language. 2007. "Covariance." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Covariance.html.
APA
Wolfram Language. (2007). Covariance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Covariance.html