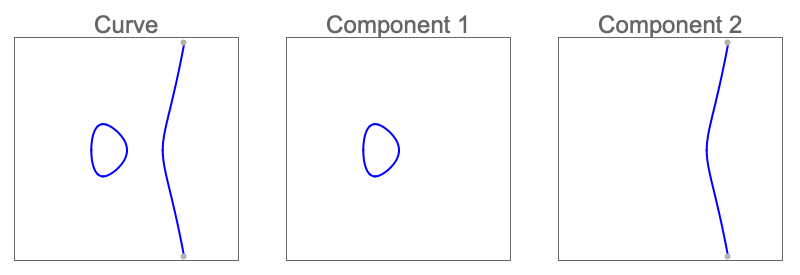
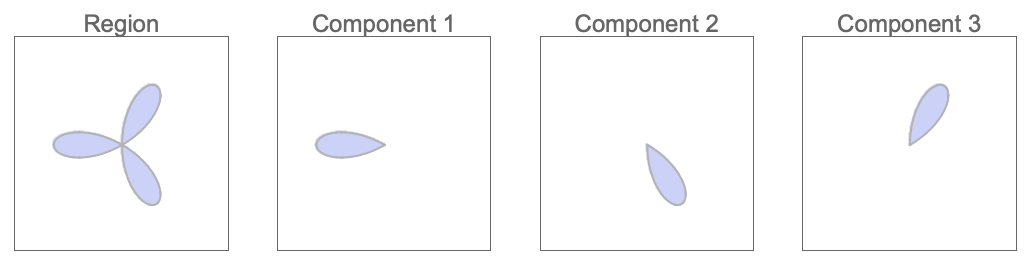
CylindricalDecomposition[expr,{x1,x2,…}]
将由语句 expr 表示的区域分解为圆柱分量,其方向依次对应于 xi.
CylindricalDecomposition[expr,{x1,x2,…},op]
求对由语句 expr 表示的区域应用拓扑运算的结果的分解.
CylindricalDecomposition[expr,{x1,x2,…},"Function"]
将结果表示为 CylindricalDecompositionFunction[…][x1,x2,…],以便有效运用于以后的计算中.


CylindricalDecomposition
CylindricalDecomposition[expr,{x1,x2,…}]
将由语句 expr 表示的区域分解为圆柱分量,其方向依次对应于 xi.
CylindricalDecomposition[expr,{x1,x2,…},op]
求对由语句 expr 表示的区域应用拓扑运算的结果的分解.
CylindricalDecomposition[expr,{x1,x2,…},"Function"]
将结果表示为 CylindricalDecompositionFunction[…][x1,x2,…],以便有效运用于以后的计算中.
更多信息和选项



- 语句 expr 可以是以下内容的逻辑组合:
-
lhs==rhs 等式 lhs!=rhs 非等式 lhs>rhs 或 lhs>=rhs 不等式 CylindricalDecompositionFunction[…][x,y,…] 圆柱代数公式 ForAll[x,cond,expr] 通用量词 Exists[x,cond,expr] 存在量词 - 等式和不等式可涉及多项式、有理函数或实代数函数.
- CylindricalDecomposition 假定所有的变量都是实数.
- CylindricalDecomposition 返回不等式,其边界通常包含代数函数.
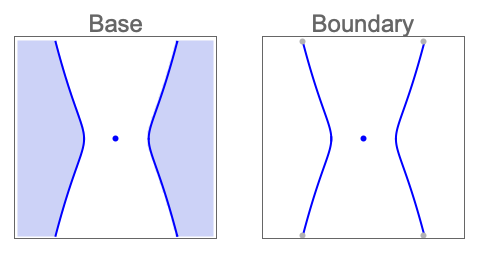
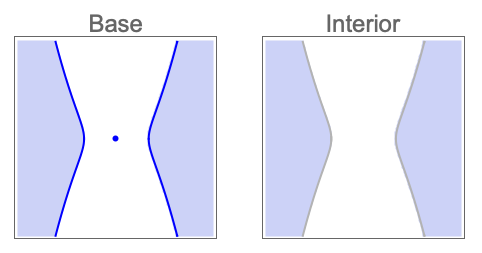
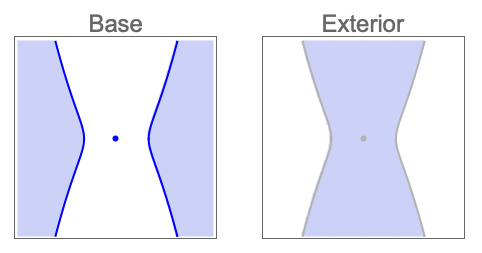
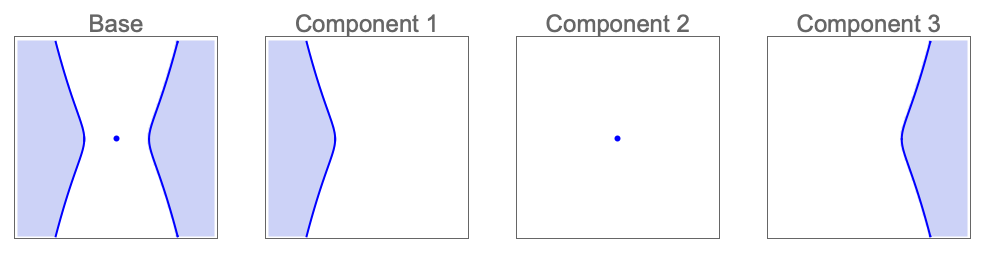
- 拓扑运算 op 可以是下列任何一种:
-
"Boundary" 解集的边界 "Closure" 解集的闭包 "Interior" 解集的内部 "Exterior" 解集的外部 "ClosureOfInterior" 解集内部的闭包 "InteriorOfClosure" 解集闭包的内部 "Components" 解集的连通分量 - CylindricalDecompositionFunction 对象提供半代数集的显式紧凑表示,可有效运用于以后的计算中.
- CylindricalDecompositionFunction 对象通常用于半代数集的重复计算,包括计算集合的布尔组合,用附加条件限制集合,消除一些变量或优化集合.
- 含有 x1,…,xn 的圆柱代数公式的形式为
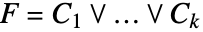 ,其中
,其中 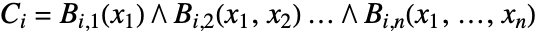 . 每个
. 每个  的形式为
的形式为  或
或 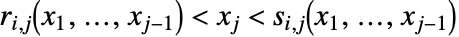 ,其中
,其中 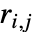 和
和 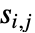 是在解集
是在解集 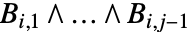 上定义并连续的代数函数.
上定义并连续的代数函数. 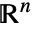 中的
中的 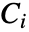 的解集
的解集 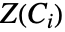 被称为 cell. 当
被称为 cell. 当 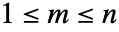 时,cell
时,cell 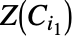 和
和 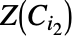 在
在 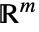 上的投影要么不相交,要么相同.
上的投影要么不相交,要么相同. - 如果没有指定 "Function",CylindricalDecomposition 返回以等式或不等式的布尔组合给出的圆柱代数公式.
- CylindricalDecompositionFunction 给出圆柱代数公式的压缩 (encapsulated) 表示,当用于 CylindricalDecomposition 的输入时,或用于如 Reduce、Resolve、FindInstance、Solve 或 Minimize 这样的求解器时会更加高效.
- Normal 将 CylindricalDecompositionFunction 对象转换成等式或不等式的布尔组合.
- 可将拓扑运算的指定和输出格式组合在一起,如 CylindricalDecomposition[ineqs,{x1,x2,…},"BoundaryFunction"] 给出了解集的边界,并将解集 ineqs 表示为 CylindricalDecompositionFunction 对象.
范例
打开所有单元 关闭所有单元范围 (14)
基本用途 (9)
利用 RegionPlot 绘制各个柱形:
CylindricalDecomposition 接受量化的公式:
选项 (1)
WorkingPrecision (1)
下面用 WorkingPrecision->1000, 得出一个分解,但结果可能是不正确的:
属性和关系 (8)
利用 RegionPlot 图形显示二维半代数集:
利用 RegionPlot3D 图形显示三维半代数集:
Resolve 完成量词消去,并且可以避免计算柱形分解:
Reduce 也处理不同的定义域和超越函数:
利用 FindInstance 得出满足方程式和不等式的点:
SemialgebraicComponentInstances 将给出每一个柱体中的样本点:
CylindricalDecomposition 合并若干柱体以得到更紧凑的表达式:
GenericCylindricalDecomposition 将仅仅计算全维数部分:
可能存在的问题 (2)
技术笔记
历史
2003年引入 (5.0) | 在以下年份被更新:2017 (11.2) ▪ 2020 (12.2)
文本
Wolfram Research (2003),CylindricalDecomposition,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CylindricalDecomposition.html (更新于 2020 年).
CMS
Wolfram 语言. 2003. "CylindricalDecomposition." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/CylindricalDecomposition.html.
APA
Wolfram 语言. (2003). CylindricalDecomposition. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CylindricalDecomposition.html 年
BibTeX
@misc{reference.wolfram_2025_cylindricaldecomposition, author="Wolfram Research", title="{CylindricalDecomposition}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CylindricalDecomposition.html}", note=[Accessed: 04-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_cylindricaldecomposition, organization={Wolfram Research}, title={CylindricalDecomposition}, year={2020}, url={https://reference.wolfram.com/language/ref/CylindricalDecomposition.html}, note=[Accessed: 04-February-2026]}