DaubechiesWavelet

DaubechiesWavelet[]

次数2のDaubechiesウェーブレットを表す．

DaubechiesWavelet[n]

次数 n のDaubechiesウェーブレットを表す．

詳細

  • DaubechiesWaveletは直交ウェーブレット族を定義する．
  • DaubechiesWavelet[n]は任意の正の整数 n について定義される．
  • スケーリング関数(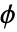)とウェーブレット関数(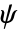)は長さ2n のコンパクトサポートを持つ．スケーリング関数は n 個のバニッシングモーメントを持つ．
  • DaubechiesWaveletはDiscreteWaveletTransform，WaveletPhi等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (3)

スケーリング関数：

ウェーブレット関数：

フィルタ係数：

スコープ  (14)

基本的な用法  (8)

主ローパスフィルタ係数を計算する：

主ハイパスフィルタ係数：

リフティングフィルタ係数：

関数を生成してリフティングウェーブレット変換を計算する：

次数2のDaubechiesスケーリング関数：

次数6のDaubechiesスケーリング関数：

異なる再帰のレベルでウェーブレット関数をプロットする：

次数2のDaubechiesウェーブレット関数：

次数6のDaubechiesWavelet：

異なる再帰のレベルでウェーブレット関数をプロットする：

ウェーブレット変換  (5)

DiscreteWaveletTransformを計算する：

ウェーブレット係数の木を見る：

ウェーブレット係数の次元を得る：

ウェーブレット係数をプロットする：

DiscreteWaveletPacketTransformを計算する：

ウェーブレット係数の木を見る：

ウェーブレット係数の次元を得る：

ウェーブレット係数をプロットする：

StationaryWaveletTransformを計算する：

ウェーブレット係数の木を見る：

ウェーブレット係数の次元を得る：

ウェーブレット係数をプロットする：

StationaryWaveletPacketTransformを計算する：

ウェーブレット係数の木を見る：

ウェーブレット係数の次元を得る：

ウェーブレット係数をプロットする：

LiftingWaveletTransformを計算する：

ウェーブレット係数の木を見る：

ウェーブレット係数の次元を得る：

ウェーブレット係数をプロットする：

より高い次元  (1)

多変量スケーリング関数と多変量ウェーブレット関数はそれぞれの一変量関数の積である：

アプリケーション  (3)

Daubechiesウェーブレット係数を使って関数を近似する：

LiftingWaveletTransformを行う：

n 個の最大係数を保ちその他すべてを閾値化することでもとのデータを近似する：

他の近似と比較する：

インパルスを含む信号の多重解像度表現を計算する：

信号の累積エネルギーをそのウェーブレット係数と比較する：

信号の順序化された累積エネルギーを計算する：

信号のエネルギーは比較的少ないウェーブレット係数で捉えられる：

特性と関係  (13)

DaubechiesWavelet[1]はHaarWaveletに等しい：

ローパスフィルタ係数の総和は単位元である．：

ハイパスフィルタ係数の総和は0である．：

スケーリング関数を積分すると単位元になる．：

とりわけ ：

ウェーブレット関数を積分すると0になる．：

ウェーブレット関数は同じスケールのスケーリング関数と直交する．：

ローパスフィルタ係数とハイパスフィルタ係数は直交する．：

DaubechiesWavelet[n]は n 個のバニッシングモーメントを持つ．：

これは，線形信号はそのようなスケーリング関数のパート({0})で完全に表される事を意味する：

二次，あるいはそれより高次の信号はそうではない：

は再帰方程式 を満足する：

構成要素と再帰の総和をプロットする：

は再帰方程式 を満足する：

構成要素と再帰の総和をプロットする：

に対する周波数応答は で与えられる：

フィルタはローパスフィルタである：

次数 n が高くなるにつれ，最後の応答関数は平坦になる：

のフーリエ(Fourier)変換はで与えられる：

に対する周波数応答はで与えられる：

フィルタはハイパスフィルタである：

次数 n が高くなるにつれ，最後の応答関数は平坦になる：

のフーリエ変換は で与えられる：

おもしろい例題  (2)

スケーリング関数の平行移動と膨張をプロットする：

ウェーブレット関数の平行移動と膨張をプロットする：

Wolfram Research (2010), DaubechiesWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/DaubechiesWavelet.html.

テキスト

Wolfram Research (2010), DaubechiesWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/DaubechiesWavelet.html.

CMS

Wolfram Language. 2010. "DaubechiesWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DaubechiesWavelet.html.

APA

Wolfram Language. (2010). DaubechiesWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DaubechiesWavelet.html

BibTeX

@misc{reference.wolfram_2024_daubechieswavelet, author="Wolfram Research", title="{DaubechiesWavelet}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/DaubechiesWavelet.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_daubechieswavelet, organization={Wolfram Research}, title={DaubechiesWavelet}, year={2010}, url={https://reference.wolfram.com/language/ref/DaubechiesWavelet.html}, note=[Accessed: 14-November-2024 ]}