DegreeCentrality

DegreeCentrality[g]

给出 g 的基本简单图中顶点的顶点度列表.

DegreeCentrality[g,"In"]

给出顶点的入度列表.

DegreeCentrality[g,"Out"]

给出顶点的出度列表.

DegreeCentrality[{vw,…},…]

用规则 vw 指定图 g.

更多信息

  • DegreeCentrality 对具有较高顶点度的顶点给出高中心度.
  • 顶点 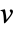的顶点度是与 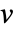相关联的边数.
  • 对于一个有向图，入度是入边的数目，而出度是出边的数目.
  • 对于一个无向图，入度和出度一致.
  • DegreeCentrality 适用于无向图、有向图、多重图和混合图.

范例

打开所有单元关闭所有单元

基本范例  (2)

计算度中心度：

突出显示：

对顶点排序. 排在最前面的顶点与其他顶点具有最多的连接数：

范围  (7)

DegreeCentrality 可用于无向图：

有向图：

多重图：

混合图：

用规则指定图：

计算入度和出度：

DegreeCentrality 可用于大规模图：

应用  (8)

根据顶点对邻域内其他顶点的影响排序：

突出显示 CycleGraph 的度中心度：

GridGraph：

CompleteKaryTree：

PathGraph：

学校里的朋友关系网络. 求最受欢迎的学生：

arXiv电子打印存档中的《高能物理现象》部分的引文网络，排名前10位被引用最多的文章：

求食物链中的基位种或者生产者:

求顶级物种或顶点捕食者：

2011年11月发送给 MathGroup 列表的电子邮件列表网络. 构建用户的社交网络，如果 已经发送至少一条回复给 ，则构建一条从 到 的边. 求最积极回复邮件的用户：

计算接受回复但是没有回复其他人的用户数目：

求最经常问问题的用户：

计算只发送回复没有接受任何回复的用户数目：

在自治系统水平上的因特网. 度中心的频率服从幂律分布：

假定齐夫分布，获得最大似然参数估计：

概率密度函数：

对于具有 个顶点的图，最中心顶点和所有其他顶点之间的度中心度差值的最大和是 :

测量最中心的顶点关于其他顶点的中心度：

社交网络的中心化处理：

属性和关系  (5)

一个无向图的顶点度是与该顶点相关联的边数：

对于无向图，入度中心度和出度中心度必须一致：

使用 VertexDegree 来获得特定顶点的度数：

对于简单图，DegreeCentrality 等于 VertexDegree：

对于一个有向图，入度中心度和出度中心度的和等于顶点度：

Wolfram Research (2010)，DegreeCentrality，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DegreeCentrality.html （更新于 2015 年）.

文本

Wolfram Research (2010)，DegreeCentrality，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DegreeCentrality.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "DegreeCentrality." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/DegreeCentrality.html.

APA

Wolfram 语言. (2010). DegreeCentrality. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DegreeCentrality.html 年

BibTeX

@misc{reference.wolfram_2024_degreecentrality, author="Wolfram Research", title="{DegreeCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DegreeCentrality.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_degreecentrality, organization={Wolfram Research}, title={DegreeCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/DegreeCentrality.html}, note=[Accessed: 21-November-2024 ]}