EccentricityCentrality

EccentricityCentrality[g]

给出图 g 中顶点的偏心率中心性列表.

EccentricityCentrality[{vw,…}]

用规则 vw 指定图 g.

更多信息

  • EccentricityCentrality 给出与每个其它可达到的顶点具有最短最大距离的顶点的高中心性.
  • 图 g 的 EccentricityCentrality 由 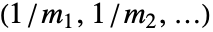给出，其中 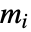是从顶点 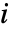到所有与 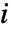相连的顶点的最大距离.
  • 孤立顶点的偏心率中心性为零.
  • EccentricityCentrality 可用于无向图、有向图、加权图、多重图和混合图.

背景

  • EccentricityCentrality 返回一个由非负机器精度数值构成的列表（“偏心率中心度”）作为图顶点的某种特定的中心性度量的近似值. 偏心率中心度是对网络中一个结点的中心性的度量，这个值基于从一个顶点 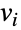到所有其它可达结点的最短距离中的最大值（即图偏心率）. 这一度量在社交网络、交通、生物学和社会科学中都有应用.
  • 若 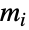是从顶点 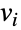到所有其它与之相连的顶点的最大距离，那么偏心率中心度就是 . 孤立顶点的偏心率中心度为零. 偏心率中心度介于 0 和 1 之间（包括两端）.
  • 一个顶点的偏心率中心度是其 VertexEccentricity 的倒数. 图的全距离矩阵可以用 GraphDistanceMatrix 计算.

范例

打开所有单元关闭所有单元

基本范例  (2)

计算偏心率中心性：

突出显示：

对顶点排序. 排序在前面的顶点位于其它每个可达到顶点的短距离内：

范围  (7)

EccentricityCentrality 可用于无向图：

有向图：

加权图：

多重图：

混合图：

用规则指定图：

EccentricityCentrality 可用于大规模图：

应用  (5)

按偏心率对顶点排序：

突出显示 CycleGraph 的偏心率中心性：

GridGraph:

CompleteKaryTree:

PathGraph:

在 Micronesia 东部的 Marshall 群岛的基建网络基础上，找到一个经过策略布局的岛屿：

它与图的中位数不同：

连接芝加哥郊区的公路网络. 求医院和消防部门的最佳位置，以最小化紧急车辆行驶的距离：

对于具有 个距离的图，最中心的顶点和所有其他顶点之间的偏心率差异的最大和是 的倒数：

测量最中心的顶点关于其他顶点的中心度：

将社会网络中心化处理：

属性和关系  (6)

EccentricityCentrality 是与其他可达到顶点的最大距离的逆：

与其他可达到顶点的最大距离的逆：

顶点的偏心率中心性是 VertexEccentricity 的倒数：

偏心率中心性位于0和1之间：

无向图的偏心率中心性等于每个分量的中心性：

计算每个分量的中心性给出相同结果：

使用 GraphCenter 求具有最高偏心率中心性的顶点：

使用 VertexIndex 获取特定顶点的中心性：

Wolfram Research (2012)，EccentricityCentrality，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EccentricityCentrality.html （更新于 2015 年）.

文本

Wolfram Research (2012)，EccentricityCentrality，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EccentricityCentrality.html （更新于 2015 年）.

CMS

Wolfram 语言. 2012. "EccentricityCentrality." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/EccentricityCentrality.html.

APA

Wolfram 语言. (2012). EccentricityCentrality. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EccentricityCentrality.html 年

BibTeX

@misc{reference.wolfram_2024_eccentricitycentrality, author="Wolfram Research", title="{EccentricityCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EccentricityCentrality.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_eccentricitycentrality, organization={Wolfram Research}, title={EccentricityCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/EccentricityCentrality.html}, note=[Accessed: 21-November-2024 ]}