EigenvectorCentrality

EigenvectorCentrality[g]

给出图 g 中的顶点的特征向量中心度列表.

EigenvectorCentrality[g,"In"]

给出有向图 g 的内中心度列表.

EigenvectorCentrality[g,"Out"]

给出有向图 g 的外中心度列表.

EigenvectorCentrality[{vw,…},…]

用规则 vw 指定图 g.

更多信息和选项

  • EigenvectorCentrality 对于与许多其他连接度很好的顶点相连接的顶点，给出高中心度.
  • EigenvectorCentrality 给出中心度 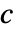组成的列表，这些中心度可以表示为邻节点的中心度的加权和.
  • 当 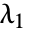是图 g 中邻接矩阵 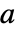的最大特征值时，我们有：
  • EigenvectorCentrality[g]c=TemplateBox[{{{1, /, {lambda, _, 1}}, a}}, Transpose].c
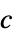    EigenvectorCentrality[g,"In"]c=TemplateBox[{{{1, /, {lambda, _, 1}}, a}}, Transpose].c， 左特征向量
    EigenvectorCentrality[g,"Out"]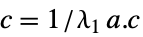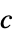， 右特征向量
  • 特征向量中心度是经过规范化处理的.
  • 对于有向图 g，EigenvectorCentrality[g] 等价于 EigenvectorCentrality[g,"In"].
  • 选项 WorkingPrecision->p 可用于控制在内部计算中所用的精度.
  • EigenvectorCentrality 作用于无向图、有向图、多重图和混合图.

范例

打开所有单元关闭所有单元

基本范例  (2)

计算特征向量中心度：

突出显示：

对顶点排序. 与许多连接度很好的顶点相连接的顶点排在最前面.

范围  (7)

EigenvectorCentrality 可用于无向图：

有向图：

多重图：

混合图：

用规则指定图：

计算入度中心度和出度中心度：

EigenvectorCentrality 作用于大规模图：

选项  (3)

WorkingPrecision  (3)

默认情况下，EigenvectorCentrality 利用机器精度计算求中心度：

指定较高的工作精度：

无穷大的工作精度对应于精确计算：

应用  (9)

根据与其他连接度很好的顶点的连接度，对顶点排序：

按照从最高到最低中心度，对顶点排序：

突出显示 CycleGraph 的特征向量中心度：

GridGraph:

CompleteKaryTree:

PathGraph:

求一个社交网络中连接度良好的人员：

突出显示该网络：

如果 A 学生咨询 B 学生的意见，求从 A 学生到 B 学生具有链接的学生会网络中最有影响力的成员：

存档的高能物理现象部门的引用文献网络. 求排名前10的重要文献：

在自治系统水平，求网络的核心节点：

核心节点是连通度良好的顶点，并且具有最高特征向量中心度：

求一个蛋白质，删除蛋白质后将导致酵母的蛋白质交互网络中出现致命性：

具有最大特征向量中心度的蛋白质：

删除蛋白质增加了网络的半径：

Saccharomyces cerevisiae 蛋白质交互网络. 特征向量中心度的频率服从幂律分布：

假定采用齐夫分布，获得最大似然参数估计：

概率密度函数：

某组织的人机系统处理网络订单，并且通过邮件发送货物. 求应该给予最多资源的部门：

大部分服务依赖于系统管理部门，以及注册订单部门：

属性和关系  (6)

对于无向图，中心度向量 满足方程 ：

对于有向图，入度向量 满足方程 :

出度中心度向量 满足方程 ：

特征向量中心度被规范化处理：

对于非连通图，中心度关于连通分量进行规范化处理：

由连接分量生成的子图的中心度：

EigenvectorCentrality 是 KatzCentrality 的一个特例：

将 和 作为 KatzCentrality 的参数使用：

使用 VertexIndex 获取特定顶点的中心度：

Wolfram Research (2010)，EigenvectorCentrality，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EigenvectorCentrality.html （更新于 2015 年）.

文本

Wolfram Research (2010)，EigenvectorCentrality，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EigenvectorCentrality.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "EigenvectorCentrality." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/EigenvectorCentrality.html.

APA

Wolfram 语言. (2010). EigenvectorCentrality. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EigenvectorCentrality.html 年

BibTeX

@misc{reference.wolfram_2024_eigenvectorcentrality, author="Wolfram Research", title="{EigenvectorCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EigenvectorCentrality.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_eigenvectorcentrality, organization={Wolfram Research}, title={EigenvectorCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/EigenvectorCentrality.html}, note=[Accessed: 21-November-2024 ]}