Element

Element[x,dom]

または x∈dom は，x が領域 dom の要素であることを宣言する．

Element[x,reg]

または x∈reg は，x が領域 reg の要素であることを宣言する．

Element[x1|x2|…,dom]

すべての xiが dom の要素であることを宣言する．

Element[patt,dom]

パターン patt にマッチする任意の式が dom の要素であることを宣言する．

詳細

  • x∈dom は，x el dom または x \[Element] dom として入力できる．
  • Elementは，Simplifyおよび関連する関数の仮定を設定するのに使用される．
  • dom は，数値領域あるいは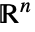における領域である．
  • 可能な領域 dom
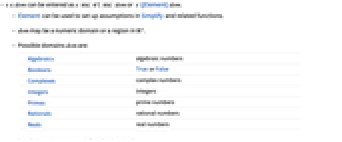
  • Algebraics代数的数
    BooleansTrueまたはFalse
    Complexes複素数
    Integers整数
    Primes素数
    Rationals有理数
    Reals実数
  • 可能な領域 reg はRegionQによって定義される．
  • x が数値の場合，x∈dom は，可能なら直ちに評価される．
  • 領域 dom については，{x1,x2,…}∈domは(x1|x2|…)∈dom と同等である．
  • 領域 reg については，{x1,x2,…}∈reg は座標x1,x2,…の点は reg に属すると宣言する．
  • {x1,x2,…}∈dom は，真偽が直ちに決定できない場合，(x1|x2|…)∈dom に評価される．

例題

すべて開くすべて閉じる

例  (5)

が実数の要素かどうかの検定を行う：

点が単位円板に属するかどうかの検定を行う：

式の領域構成を表す：

点 が単位球体に属すると宣言する：

要素の宣言を使って領域上で積分する：

あるいは，領域上で最適化する：

elemを使って入力する：

スコープ  (9)

領域構成の検定を行う：

領域の帰属判定：

これをプロットする：

領域構成の仮定をする：

領域の帰属関係を表す：

仮定を使って領域構成の検定を行う：

仮定を使って領域の帰属判定を行う：

変数の領域を指定する：

パターンにマッチするオブジェクトの仮定を指定する：

TraditionalFormによる表示：

特性と関係  (2)

単一の変数の場合，Elementの否定は自動的にNotElementに変換される：

変数が複数の場合，Elementの否定は自動的には簡約されない：

LogicalExpandを使ってNotElementについての表現を求める：

Elementは，領域の帰属関係を宣言する：

RegionMemberは明示的な領域の帰属条件を与える：

考えられる問題  (1)

領域構成が不明の場合，Element文は評価されずに残る：

Wolfram Research (1999), Element, Wolfram言語関数， https://reference.wolfram.com/language/ref/Element.html （2014年に更新）.

テキスト

Wolfram Research (1999), Element, Wolfram言語関数， https://reference.wolfram.com/language/ref/Element.html （2014年に更新）.

CMS

Wolfram Language. 1999. "Element." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Element.html.

APA

Wolfram Language. (1999). Element. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Element.html

BibTeX

@misc{reference.wolfram_2024_element, author="Wolfram Research", title="{Element}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Element.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_element, organization={Wolfram Research}, title={Element}, year={2014}, url={https://reference.wolfram.com/language/ref/Element.html}, note=[Accessed: 21-November-2024 ]}