Fibonacci
詳細

- 記号操作・数値操作の両方に適した数学関数である.
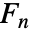 は再帰関係
は再帰関係 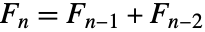 (
(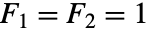 )を満たす.
)を満たす.- n を複素数としたとき,
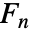 は一般式
は一般式 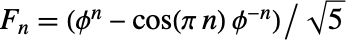 により与えられる.
により与えられる.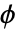 は黄金比である.
は黄金比である. - フィボナッチ多項式
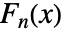 は,式
は,式 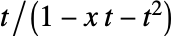 を展開することで得られる
を展開することで得られる 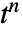 の係数である.
の係数である. - フィボナッチ多項式は再帰関係
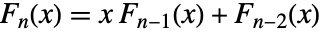 を満足する.
を満足する. - FullSimplifyおよびFunctionExpandは,引数が n∈Integersを使用して整数と指定された場合に,フィボナッチ数を記号的な引数と結合するような変換則を含んでいる.
- Fibonacciは任意の数値精度で評価できる.
- Fibonacciは自動的にリストに縫い込まれる.
- FibonacciはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開く すべて閉じる例 (6)
スコープ (43)
数値評価 (6)
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のFibonacci関数を計算することもできる:
特定の値 (6)
可視化 (5)
関数の特性 (14)
Fibonacciはすべての実数値について定義される:
Fibonacciの近似関数の値域:
Fibonacciは鏡特性 ![]() を持つ:
を持つ:
Fibonacciは要素単位でリストに縫い込まれる:
Fibonacciは x の解析関数である:
Fibonacciは奇数値については非減少でも非増加でもない:
Fibonacciは偶数値については非減少である:
Fibonacciは奇数値については単射ではない:
Fibonacciは奇数値については全射ではない:
Fibonacciは奇数値については非負である:
Fibonacciは特異点も不連続点も持たない:
Fibonacciは奇数値について凸である:
TraditionalFormによる表示:
積分 (3)
級数展開 (4)
関数の恒等式と簡約 (2)
アプリケーション (13)
特性と関係 (15)
フィボナッチ数 (13)
MatrixPowerを使った閉形の解:
FibonacciはDifferenceRootとして表すことができる:
Fibonacciの級数展開における一般項:
Fibonacciの母関数:
FindSequenceFunctionはFibonacci数列を認識する:
Fibonacciの指数母関数:
考えられる問題 (3)
テクニカルノート
履歴
1996 で導入 (3.0) | 1999 で更新 (4.0) ▪ 2000 (4.1) ▪ 2002 (4.2)
テキスト
Wolfram Research (1996), Fibonacci, Wolfram言語関数, https://reference.wolfram.com/language/ref/Fibonacci.html (2002年に更新).
CMS
Wolfram Language. 1996. "Fibonacci." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/Fibonacci.html.
APA
Wolfram Language. (1996). Fibonacci. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Fibonacci.html
BibTeX
@misc{reference.wolfram_2025_fibonacci, author="Wolfram Research", title="{Fibonacci}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/Fibonacci.html}", note=[Accessed: 02-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_fibonacci, organization={Wolfram Research}, title={Fibonacci}, year={2002}, url={https://reference.wolfram.com/language/ref/Fibonacci.html}, note=[Accessed: 02-March-2026]}



