FinancialBond
FinancialBond[params,ambientparams]
给出金融债券工具的值.
FinancialBond[params,ambientparams,prop]
计算指定属性 prop.
更多信息和选项




- FinancialBond 作为一种金融工具,涉及一系列利息支付与到期时的本金支付.
- FinancialBond 可用于数值型表达式或任意符号式表达式.
- FinancialBond[params,ambientparams,{prop1,prop2,…}] 计算多个属性,并将结果以列表的形式返回.
- FinancialBond[params,ambientparams,"Rules"] 计算全部可用属性.
- FinancialBond 中的参数全部以规则集合 {param1,val1,param2,val2,…}] 的形式给出.
- 可能的参数包括:
-
"FaceValue" 票面价值或面值 "Coupon" 利息率或支付函数 "Maturity" 到期日 "CouponInterval" 付息期 "RedemptionValue" 赎回价值(如果不同于票面价值) - 可能的环境参数包括:
-
"InterestRate" 到期收益或收益率 "Settlement" 结算日期 "DayCountBasis" 天数计算约定 - 结算与到期的指定可以按照日期或绝对时间单位的形式输入.
- 利息可以以单一日期或与时间相关的支付函数的形式给出.
- 可能的利息指定包括:
-
r 单一收益率 {r1,r2,…} 应用于单位时间区间上的即期汇率表 {{t1,r1},{t2,r2},…} 在指定时间改变的利率表 {p1->r1,p2->r2,…} 利率期限结构 function 利息力,以时间函数的形式给出 - 对 "DayCountBasis" 可以进行下列设置:
-
"30/360" 美式债券 "30E/360" 欧式债券(ISDA 2006) "30E/360German" 欧式债券(ISDA 2000,德国) "30E+/360" 30E+/360 天数计算约定 "ActualICMA" 实际/实际 ICMA "ActualISDA" 实际/实际 ISDA "Actual/365" 实际/365(固定) "Actual/360" 实际/360(法国) "Actual/365L" 实际/365L "ActualAFB" 实际/实际 AFB/FBF 主协定 Automatic 精确的历法计算 - FinancialBond 可以计算下列属性:
-
"Value" 根据应计利息调整的价格 "FullValue" 未调整价格 "AccruedInterest" 结算时的应计利息 "Duration" 麦考利(Macaulay)久期 "ModifiedDuration" 修正久期 "Convexity" 凸性 "CouponPeriodDays" 包含结算日在内的付息期天数 "CouponToSettlementDays" 从前一个付息日到结算日的天数 "SettlementToCouponDays" 从结算日到下一个付息日的天数 "NextCouponDate" 下一个付息日 "PreviousCouponDate" 前一个付息日 "RemainingCoupons" 剩余息票支付 "AccruedFactor" 表示应计利息的息票支付分数 - 如果在 FinancialBond 中使用的是到期日为
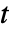 的抽象时间单位,则指定的结算时间
的抽象时间单位,则指定的结算时间 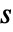 必须位于债券存在范围之间(
必须位于债券存在范围之间(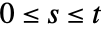 ).
). - 按照惯例,到期收益率与息票支付为名义算法,复利区间等于利息支付区间. 通过使用 EffectiveInterest 函数或函数式利率指定,可以得到任意复利方式的结果.
- 如果息票区间为 q,则息票支付发生在时刻 q、2q …. 如果没有给出息票区间,则认为支付发生在时刻 1、2 …. 在设置为 "CouponInterval"->0 时,认为由 "Coupon"->f 指定的函数是连续的.
- 如果日期在 FinancialBond 中指定,并且以函数形式指定了息票或利率,或者利率以列表或期限结构的形式指定,则函数认为时刻0发生在距结算日最近的时间点,且结算日表示的是从到期日算起的整数年.
- 支付函数可以根据递归关系给出. RSolve 可用于将递归关系转换为时间函数,以在 FinancialBond 中使用.
- 当抽象时间单位用于 FinancialBond 时,历法属性不适用.
- 可以给出下列选项:
-
Assumptions $Assumptions 对参数所做的假定 GenerateConditions False 是否生成关于参数的关系
范例
打开所有单元关闭所有单元基本范例 (6)
范围 (9)
FinancialBond 可用于符号参数,并得到闭合形式的表达式:
Apart 可将贴现因子系数应用于单个支付:
可能需要多次应用 Apart 以将表达式完全分解:
可以求得涉及 FinancialBond 的方程的符号解:
可以为 FinancialBond 提供一个利率期限结构或未来即期利率的列表:
当日期及随时间变化的利率结构已知,则认为时刻0发生在结算日期前的最近的时间点,并且该时间点距到期日为整数年. 在该例中,时刻0为2010年12月31日:
FinancialBond 可以取一个函数式(增长)的利息及利息力:
永续债券(console bond) 可用 Infinity 作为到期日来定价:
推广和延伸 (5)
FinancialBond 取名义收益率,并假定复利频率等于息票频率. 然而,有时可能使用不同的复利频率更为理想. 可以可以使用 EffectiveInterest 在息票频率下计算复利后给出正确实际贴现的利率:
已知一债券的面值为$1000,可在10年到15年之间的某个未知时刻以$1100兑付. 可以使用 Expectation 求该债券价格的期望值:
当期限结构已知时,可以使用 EffectiveInterest 确定用于 FinancialBond 的实际贴现率:
可以使用 RSolve 将递归关系转换为单独的时间函数:
上面的递归关系代表每次支付时按固定速率增加的支付. 它的解是一个仅关于时间的函数,适合在 FinancialBond 中使用:
应用 (7)
一零息债券将在十年底支付$1000,当前售价为$400. 求半年复利的隐含收益率:
已知一10年债券的面值为$1000,付息期为每年,按通胀调整,初始息票利率为7%,每期息票比前期增长3%. 且赎回价值为$1200,求该债券的价格:
一面值$100,付息期为半年,息票利率为8%的债券在5月1日发行,在大约2年后的5月15日,该债券的售价为$88. 求此日按精确的历法计算时的收益率:
一付息期为半年的可赎回债券,在赎回价值为$1200,赎回日期为2020年12月31日,结算日期为2010年7月12日的价格:
在 "30/360" 天数计算约定的条件下,一按季付息、息票利率为4%、到期日为2030年12月31日且结算日为2013年9月5日的债券距下一次付息日的天数:
一半年付息的20年期债券的名义利率为8%,价格为$1722.25. 从15年底后,该债券可在任意付息日按债券面值赎回. 求能够保证收益率至少为6%的票面价值:
求同一债券在面值为$1000、价格为$1300的条件下保证收益率不低于7%时的赎回价格:
如果该债券的赎回价格为$1000、价格为$900,求投资者有希望达到的最大收益率:
某债券的付息期为半年,到期日为2030年12月31日,结算日期为2010年11月12日,利用 "Actual/360" 天数计算约定,求该债券的久期与凸性:
属性和关系 (2)
久期与凸性可以利用符号收益与导函数 D 手动计算得到:
利用 FinancialBond 属性计算上面的两个量:
在付息日时,FinancialBond 对象的价值将给出与 Annuity 对象相同的价值,如果后者具有相同的支付频率以及与债券面值相等的最终支付:
可能存在的问题 (1)
尽管债券可以定义为具有最终支付的年金,FinancialBond 给出的是一个价格,而 TimeValue 给出的是 Annuity 按时间定价的等价物. 在计算现值时(时刻=0),两者没有差异,但在其它非零时段时两者是不同的:
巧妙范例 (2)
文本
Wolfram Research (2010),FinancialBond,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FinancialBond.html.
CMS
Wolfram 语言. 2010. "FinancialBond." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FinancialBond.html.
APA
Wolfram 语言. (2010). FinancialBond. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FinancialBond.html 年