FindFormula
FindFormula[data]
找到一个逼近 data 的纯函数
FindFormula[data,x]
找到一个变量为 x 的逼近 data 的符号函数.
FindFormula[data,x,n]
找到最多 n 个逼近 data 的函数.
FindFormula[data,x,n,prop]
返回最多 n 个与属性 prop 相关联的最佳函数.
FindFormula[data,x,n,{prop1,prop2,…}]
返回最多 n 个与属性 prop1、prop2 等相关联的最佳函数.
更多信息和选项

- 数据应为 {{x1,y1},{x2,y2},…} 或 {y1,y2,…} 形式的数组,或者是 TimeSeries 对象.
- {y1,y2,…} 形式的数据等价于 {{1,y1},{2,y2},…} 形式的数据.
- FindFormula[data,x,n,All] 创建具备所有可能属性的 Dataset 对象.
- 支持的属性包括:
-
"Score" 内部得分 "Complexity" 函数的复杂性 "Error" 均方误差 All 所有前述属性 - 可以给出以下选项:
-
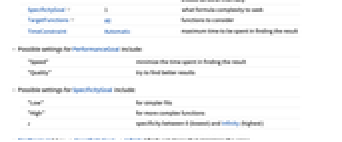
PerformanceGoal Automatic 要优化的性能方面 RandomSeeding Automatic 应该在内部对伪随机数生成器进行什么样的初始化 SpecificityGoal 1 - 查找何种公式复杂性
TargetFunctions All 要考虑的函数 TimeConstraint Automatic 查找结果可用的最大时间 - PerformanceGoal 的可能设置包括:
-
"Speed" 最小化花在查找结果上的时间 "Quality" 尝试查找更佳结果 - SpecificityGoal 的可能设置包括:
-
"Low" 更简单的拟合 "High" 更复杂的函数 s 在 0 (最低) 和 Infinity (最高)之间指定 - FindFormula[data,x,SpecificityGoal->Infinity] 寻找使误差最小化的解.
- SpecificityGoal 等于1时给出最佳的预测性能.
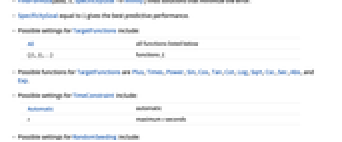
- TargetFunctions 的可能设置包括:
-
All 所有下列的函数 { 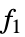 ,
,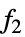 ,…}
,…}函数 
- TargetFunctions 可能的函数有 Plus、Times、Power、Sin、Cos、Tan、Cot、Log、Sqrt、Csc、Sec、Abs 和 Exp.
- TimeConstraint 的可能设置包括:
-
Automatic 自动的 t 最大 t 秒 - RandomSeeding 的可能设置包括:
-
Automatic 每次函数调用时自动重新播种 Inherited 使用外部播种的随机数字 seed 用明确给定的整数或字符串作为种子
范例
打开所有单元关闭所有单元基本范例 (2)
范围 (3)
查看前 300 个拟合,并且对 SpecificityGoal 的不同设置,将它们的分数用误差和复杂度的函数制作图形:
选项 (4)
PerformanceGoal (1)
RandomSeeding (1)
SpecificityGoal (1)
TargetFunctions (1)
Wolfram Research (2015),FindFormula,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FindFormula.html (更新于 2017 年).
文本
Wolfram Research (2015),FindFormula,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FindFormula.html (更新于 2017 年).
CMS
Wolfram 语言. 2015. "FindFormula." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/FindFormula.html.
APA
Wolfram 语言. (2015). FindFormula. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FindFormula.html 年