FractionalGaussianNoiseProcess
FractionalGaussianNoiseProcess[μ,σ,h]
ドリフト μ,ボラティリティ σ,Hurst指数 h の非整数ガウス(Gauss)ノイズ過程を表す.
FractionalGaussianNoiseProcess[h]
ドリフト0,ボラティリティ1,Hurst指数 h の非整数ガウスノイズ過程を表す.
詳細

- FractionalGaussianNoiseProcessは,連続時間・連続状態のランダム過程である.
- FractionalGaussianNoiseProcessは,平均値関数
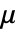 ,共分散関数
,共分散関数 ![sigma^2 (TemplateBox[{{t, -, s, -, 1}}, Abs]^(2 h)-2 TemplateBox[{{t, -, s}}, Abs]^(2 h)+TemplateBox[{{t, -, s, +, 1}}, Abs]^(2 h))/2 sigma^2 (TemplateBox[{{t, -, s, -, 1}}, Abs]^(2 h)-2 TemplateBox[{{t, -, s}}, Abs]^(2 h)+TemplateBox[{{t, -, s, +, 1}}, Abs]^(2 h))/2](Files/FractionalGaussianNoiseProcess.ja/2.png) のガウス過程である.
のガウス過程である. - FractionalGaussianNoiseProcess[μ,σ,h]はTransformedProcess[x[t+1]-x[t],xFractionalBrownianMotionProcess[μ,σ,h],t]に等しい.
- FractionalGaussianNoiseProcessでは,μ は任意の実数,σ は任意の正の実数,h は0から1までの任意の実数が許容される.
- FractionalGaussianNoiseProcessは,RandomFunction,CovarianceFunction等の関数で使うことができる.
例題
すべて開くすべて閉じるスコープ (11)
基本的な用法 (6)
過程スライス特性 (5)
CentralMomentおよびその母関数:
Cumulantおよびその母関数:
アプリケーション (1)
特性と関係 (7)
FractionalGaussianNoiseProcessは弱定常である:
平均エルゴード性を結論付けるために,積分の限界が0かどうかをチェックする:
非整数ガウスノイズは,1/2より大きいHurst母数についての長期記憶を持つ:
非弱定常FractionalBrownianMotionProcessと比較する:
テキスト
Wolfram Research (2014), FractionalGaussianNoiseProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html.
CMS
Wolfram Language. 2014. "FractionalGaussianNoiseProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html.
APA
Wolfram Language. (2014). FractionalGaussianNoiseProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html