FractionalBrownianMotionProcess
FractionalBrownianMotionProcess[μ,σ,h]
represents fractional Brownian motion process with drift μ, volatility σ, and Hurst index h.
FractionalBrownianMotionProcess[h]
represents fractional Brownian motion process with drift 0, volatility 1, and Hurst index h.
Details
- FractionalBrownianMotionProcess is also known as fractal Brownian motion or fractional Wiener process.
- FractionalBrownianMotionProcess is a continuous-time and continuous-state random process.
- FractionalBrownianMotionProcess is a Gaussian process with mean function
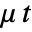and covariance function ![sigma^2 (s^(2 h)+t^(2 h)-TemplateBox[{{t, -, s}}, Abs]^(2 h))/2](Files/FractionalBrownianMotionProcess.en/2.png "sigma^2 (s^(2 h)+t^(2 h)-TemplateBox[{{t, -, s}}, Abs]^(2 h))/2")
. It reduces to a WienerProcess for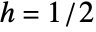 
. - FractionalBrownianMotionProcess allows μ to be any real number, σ to be any positive real number, and h to be a real number between 0 and 1.
- FractionalBrownianMotionProcess can be used with such functions as Mean, PDF, Probability, and RandomFunction.
Examples
open all close allBasic Examples (3)
Scope (11)
Basic Uses (6)
Process Slice Properties (5)
Univariate SliceDistribution:
First-order probability density function for the slice distribution:
Multivariate slice distributions:
Compute the expectation of an expression:
Calculate the probability of an event:
Skewness and kurtosis are constant:
CentralMoment and its generating function:
Cumulant and its generating function:
Properties & Relations (4)
FractionalBrownianMotionProcess is not weakly stationary:
Fractional Brownian motion does not have independent increments for 
:
Compare to the product of expectations:
Conditional cumulative probability distribution:
WienerProcess is a special case of fractional Brownian motion:
Neat Examples (3)
Simulate a fractional Brownian motion process in two dimensions:
Compare 3D behavior of fractional Brownian motion depending on the Hurst parameter:
Simulate 500 paths from a fractional Brownian motion process:
Take a slice at 1 and visualize its distribution:
Plot paths and histogram distribution of the slice distribution at 1:
Text
Wolfram Research (2012), FractionalBrownianMotionProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/FractionalBrownianMotionProcess.html.
CMS
Wolfram Language. 2012. "FractionalBrownianMotionProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FractionalBrownianMotionProcess.html.
APA
Wolfram Language. (2012). FractionalBrownianMotionProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FractionalBrownianMotionProcess.html