FractionalGaussianNoiseProcess
FractionalGaussianNoiseProcess[μ,σ,h]
表示一个分数高斯噪声过程,其中漂移为 μ,波动性为 σ,赫斯特指数为 h.
FractionalGaussianNoiseProcess[h]
表示一个分数高斯噪声过程,其中漂移为0,波动性为1,赫斯特指数为 h.
更多信息

- FractionalGaussianNoiseProcess 是一个连续时间和连续状态随机过程.
- FractionalGaussianNoiseProcess 是一个高斯过程,其中均值函数为
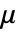 ,协方差函数为
,协方差函数为![sigma^2 (TemplateBox[{{t, -, s, -, 1}}, Abs]^(2 h)-2 TemplateBox[{{t, -, s}}, Abs]^(2 h)+TemplateBox[{{t, -, s, +, 1}}, Abs]^(2 h))/2 sigma^2 (TemplateBox[{{t, -, s, -, 1}}, Abs]^(2 h)-2 TemplateBox[{{t, -, s}}, Abs]^(2 h)+TemplateBox[{{t, -, s, +, 1}}, Abs]^(2 h))/2](Files/FractionalGaussianNoiseProcess.zh/2.png) .
. - FractionalGaussianNoiseProcess[μ,σ,h] 等价于TransformedProcess[x[t+1]-x[t],xFractionalBrownianMotionProcess[μ,σ,h],t].
- FractionalGaussianNoiseProcess 允许 μ 为任意实数,σ 为任意正实数,h 是在0到1之间的实数.
- FractionalGaussianNoiseProcess 可以和诸如 RandomFunction 和 CovarianceFunction 的函数联合使用.
范例
打开所有单元关闭所有单元范围 (11)
过程切片性质 (5)
属性和关系 (7)
Wolfram Research (2014),FractionalGaussianNoiseProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html.
文本
Wolfram Research (2014),FractionalGaussianNoiseProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html.
CMS
Wolfram 语言. 2014. "FractionalGaussianNoiseProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html.
APA
Wolfram 语言. (2014). FractionalGaussianNoiseProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FractionalGaussianNoiseProcess.html 年