Function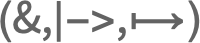

body& または Function[body]

純関数（あるいは「無名関数」）である．その形式的なパラメータは，#（または#1），#2等である．

x|->body または xbody または Function[x,body]

単一の形式的なパラメータ x を持った純関数である．

{x1,x2,…}|->body または {x1,x2,…}body または Function[{x1,x2,…},body]

形式的なパラメータのリストを持った純関数である．

Function[params,body,attrs]

評価のために属性 attrs を持つものとして扱われる純関数である．

詳細

  • Function[body]や body&が，引数の集合に適用された場合，#（または#1）は第1引数で，#2は第2引数で，と順に置換される．#0は，関数自体で置換される．
  • この関数に#i より多い数の引数が存在する場合，余分になった引数は無視される． »
  • ##は，与えられたすべての引数の列を表す． »
  • ## n は，第 n 以降の引数を表す． »
  • 連想に適用された場合，#name は#["name"]に等しく，連想中の要素を拾い出す．
  • #name の形では，name 中の文字は，任意の英数字の組合せでよいが，数字で始まってはならない．
  • 記号 は |->，fn あるいは \[Function]と入力する．
  • Functionは，LISPや形式論理学の λ に対応する．
  • Functionの属性はHoldAllである．この関数本体は，形式的なパラメータが引数と置換された後に評価される．
  • Function[{x1,…},body]の名前付きの形式的なパラメータ xiは局所的なものとして取り扱われ，関数に与えられる実際の引数との混同を避けるために必要に応じて xi$と改名される． »
  • Functionの構文はどのようにもネストすることができる．そのそれぞれが，内側の名前付き変数が必要に応じて改名されるスコープ構文として取り扱われる． »
  • Function[params, body, attrs]の attrs は，単一の属性または属性のリストよい． »
  • Function[Null,body,attrs]は，body のパラメータが#等を使って与えられる関数を表す．

例題

すべて開くすべて閉じる

例  (4)

パラメータが1つの純関数：

パラメータが2つの純関数：

を純関数に設定する：

純関数を使う：

連想から名前付きの引数を拾い出す：

スコープ  (15)

純関数を引数として使う  (5)

純関数をリストにマップする：

純関数で選択する：

純関数を述語として使う：

純関数から配列を作成する：

各要素の第2要素を比較することでソートする：

純関数をオプション値として使う  (3)

FixedPoint中でカスタム比較関数を指定する：

カスタム色関数を指定する：

カスタム距離関数を与える：

結果として純関数を返す  (4)

純関数の導関数：

Tanの導関数：

微分方程式の解が純関数で表されることがある：

差分方程式が純関数を返すことがある：

関数と連想  (3)

#name は，事実上，#["name"]の短縮形である：

#name は，常に第1引数中の連想に言及する：

1番目以外の連想スロットから抽出する：

一般化と拡張  (4)

##は全引数を表す：

## n は n 以降の引数を表す：

属性Listableを持つ純関数を作成する：

#0は純関数全体を表す：

#0を使った階乗の再帰的な定義：

アプリケーション  (3)

複数の引数を取る関数を引数のリストを取る関数に変換する：

引数をn倍する関数を返す関数：

引数を未評価の形式で保つ：

特性と関係  (11)

#1は与えられた最初の引数だけを使い，後は無視する：

引数を何も使わないと一定の純関数になる：

純関数の内部で置換を行うことができる：

混同される可能性がある場合は常に形式的なパラメータが改名される：

パラメータの名前は何でもよい：

しかし，同じ名前を使うと新たなスコープが導入される：

ネストした関数は，自分の引数を1回に1つ取る：

f[#]&は，一変数の場合には単なる f に等しい：

一般に，f[##]&は f に等しい：

変数 を含む式を純関数に変換する：

Table中の式を使う：

等価のArray式内の対応する純関数を使う：

特別目的の関数構造はInterpolatingFunctionを含む：

CompiledFunction：

NearestFunction：

LinearSolveFunction：

考えられる問題  (4)

&は->よりも緩やかに拘束するので，一般に規則中にカッコが必要である：

& による拘束は?によるものよりも弱いので，一般にパターンテストでは丸カッコが必要である：

関数が適用されるまで，Functionはその本体を評価しない：

引数の数が必要数よりも少ない場合にはエラーになる：

おもしろい例題  (2)

再帰理論の再帰演算子を定義する [詳細]：

これを使って階乗関数を定義する：

関数の零を求めるニュートン(Newton)の公式：

Wolfram Research (1988), Function, Wolfram言語関数， https://reference.wolfram.com/language/ref/Function.html （2020年に更新）.

テキスト

Wolfram Research (1988), Function, Wolfram言語関数， https://reference.wolfram.com/language/ref/Function.html （2020年に更新）.

CMS

Wolfram Language. 1988. "Function." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/Function.html.

APA

Wolfram Language. (1988). Function. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Function.html

BibTeX

@misc{reference.wolfram_2024_function, author="Wolfram Research", title="{Function}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/Function.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_function, organization={Wolfram Research}, title={Function}, year={2020}, url={https://reference.wolfram.com/language/ref/Function.html}, note=[Accessed: 21-November-2024 ]}