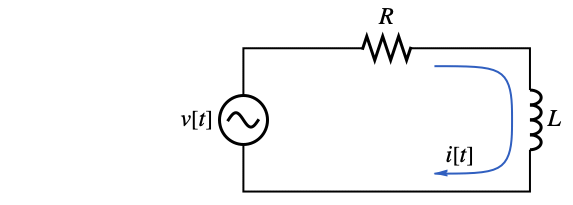
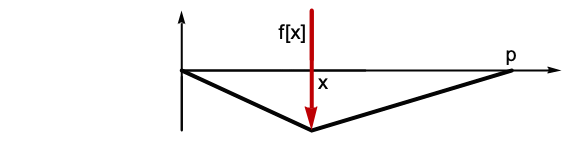
GreenFunction

GreenFunction[{ℒ[u[x]],ℬ[u[x]]},u,{x,xmin,xmax},y]

xminから xmaxまでの範囲で境界条件 ℬ を持つ線形微分演算子 ℒ についてのグリーン関数を与える．

GreenFunction[{ℒ[u[x1,x2,…]],ℬ[u[x1,x2,…]]},u,{x1,x2,…}∈Ω,{y1,y2,…}]

領域上Ωの線形偏微分演算子 ℒ についてのグリーン関数を与える．

GreenFunction[{ℒ[u[x,t]],ℬ[u[x,t]]},u,{x,xmin,xmax},t,{y,τ}]

xminから xmaxまでの範囲の線形時間依存演算子 ℒ についてのグリーン関数を与える．

GreenFunction[{ℒ[u[x1,…,t]],ℬ[u[x1,…,t]]},u,{x1,…}∈Ω,t,{y1,…,τ}]

領域Ω上の線形時間依存演算子 ℒ についてのグリーン関数を与える．

詳細とオプション

  • GreenFunctionは，インパルシブなDiracDelta駆動関数に対する系の応答を表す．
  • 微分演算子 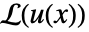についてのGreenFunctionは，与えられた非同次境界条件 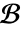を満足する L(G(x;y))=TemplateBox[{{x, -, y}}, DiracDeltaSeq]の解 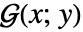であると定義できる．
  • 非同次境界条件 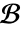がある 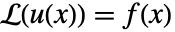の特殊解が，たたみ込み積分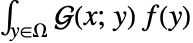を行って得ることができる．
  • 時間依存微分演算子 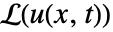についてのGreenFunctionは，指定された非同次境界条件 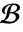を満足する L(G(x,t;y,tau))=TemplateBox[{{x, -, y}}, DiracDeltaSeq]TemplateBox[{{t, -, tau}}, DiracDeltaSeq]の解 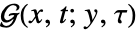として定義することができる．
  • 非同次境界条件 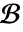を持つ 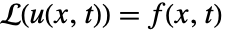の特殊解は，たたみ込み積分 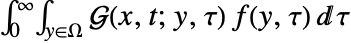を行って得ることができる．
  • 古典的な偏微分方程式のグリーン関数は，次の幾何学特性を持つ．
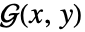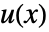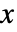  • は，従属変数が の形なら と 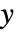の式として，従属変数の形が 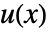ではなく 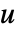なら形式パラメータ 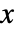と 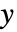を持つ純関数として与えることができる． »
  • 領域Ωは，RegionQ[Ω]がTrueとなるものなら何でもよい．
  • 常微分方程式の必要なすべての初期条件と境界条件は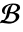， 内で指定されなければならない．
  • 偏微分方程式の境界条件は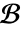， 中のDirichletConditionあるいはNeumannValueを使って指定しなければならない．
  • パラメータについての仮定はAssumptionsオプションを使って指定することができる．

例題

すべて開くすべて閉じる

例  (2)

境界値問題についてのグリーン関数：

実線上の熱演算子についてのグリーン関数：

スコープ  (22)

基本的な用法  (2)

常微分演算子についてのグリーン関数を計算する：

第2引数で u[x]の代りに u を使って結果中の純関数を得る：

偏微分演算子についてのグリーン関数を計算する：

第2引数で u[x,t]の代りに u を使って結果中の純関数を得る：

常微分方程式  (4)

初期値問題についてのグリーン関数を計算する：

ディリクレ(Dirichlet)問題についてのグリーン関数を計算する：

ノイマン(Neumann)問題についてのグリーン関数を計算する：

Robin問題についてのグリーン関数を計算する：

波動方程式  (4)

実線上の波動演算子についてのグリーン関数：

半直線上のディリクレ条件のある波動演算子についてのグリーン関数：

半直線上のノイマン条件のある波動演算子についてのグリーン関数：

区間上のディリクレ条件のある波動演算子についてのグリーン関数：

熱伝導方程式  (5)

実線上の熱演算子についてのグリーン関数：

半直線上のディリクレ条件のある熱演算子についてのグリーン関数：

区間上のディリクレ条件のある熱演算子についてのグリーン関数：

区間上のノイマン条件のある熱演算子についてのグリーン関数：

平面上の熱演算子についてのグリーン関数：

ラプラス方程式  (4)

二次元のLaplacianについてのグリーン関数：

平面の象限内のLaplacianについてのディリクレ問題：

長方形内のLaplacianについてのディリクレ問題：

三次元のLaplacianについてのグリーン関数：

ヘルムホルツ方程式  (3)

二次元のヘルムホルツ(Helmholtz)演算子についてのグリーン関数：

上半平面内のヘルムホルツ演算子についてのディリクレ問題：

長方形内のヘルムホルツ演算子についてのディリクレ問題：

オプション  (1)

Assumptions  (1)

GreenFunction内のパラメータについてのAssumptionsを指定する：

t>s という仮定の下でより単純な結果を得る：

アプリケーション  (9)

常微分方程式  (4)

GreenFunctionを使って非同次微分方程式の初期値問題を解く：

強制関数を定義する：

強制関数を使ってグリーン関数のたたみ込みを行う：

DSolveValueによる結果と比較する：

GreenFunctionを使って非同次微分方程式についてのディリクレ問題を解く：

強制関数を定義する：

強制関数を使ってグリーン関数のたたみ込みを行う：

DSolveValueによる結果と比較する：

GreenFunctionを使って非同次微分方程式についてのノイマン問題を解く：

強制関数を定義する：

強制関数を使ってグリーン関数のたたみ込みを行う：

DSolveValueによる結果と比較する：

GreenFunctionを使って非同次微分方程式についてのRobin問題を解く：

強制関数を定義する：

強制関数を使ってグリーン関数のたたみ込みを行う：

DSolveValueによる結果と比較する：

偏微分方程式  (2)

GreenFunctionを使って非同次波動方程式を解く：

非同次項を定義する：

を使って非同次方程式を解く：

DSolveValueによる解と比較する：

GreenFunctionを使って熱伝導方程式についての初期値問題を解く：

初期値を指定する：

を使って初期値問題を解く：

DSolveValueによる解と比較する：

物理と工学  (3)

抵抗RとインダクタLに繋がれた，電源が v[t]の回路内の電流 i[t]を計算する．この回路の演算子は以下で与えられる：

この回路の略図：

グリーン関数を計算する：

指定された電源での電流を求める：

2端点が固定されていて，f[x]の単位長あたりの力の影響を受ける，長さ p，張力Tの紐について，変位 u[x]を計算する．変位の演算子は以下で与えられる：

示力図：

グリーン関数を計算する：

指定された力についての変位を求める：

連続線形時不変系のインパルス応答は，系のグリーン関数を非同次初期条件とともに使って求めることができる．以下で定義される系のインパルス応答を計算する：

非同次初期条件を持つこの系のグリーン関数：

s=0と設定してインパルス応答を得る：

インパルス応答をプロットする：

特性と関係  (2)

微分方程式のグリーン関数を計算する：

DSolveを使って同じ結果を得る：

GreenFunctionはOutputResponseおよびTransferFunctionModelと関係がある：

Wolfram Research (2016), GreenFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/GreenFunction.html.

テキスト

Wolfram Research (2016), GreenFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/GreenFunction.html.

CMS

Wolfram Language. 2016. "GreenFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GreenFunction.html.

APA

Wolfram Language. (2016). GreenFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GreenFunction.html

BibTeX

@misc{reference.wolfram_2024_greenfunction, author="Wolfram Research", title="{GreenFunction}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GreenFunction.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_greenfunction, organization={Wolfram Research}, title={GreenFunction}, year={2016}, url={https://reference.wolfram.com/language/ref/GreenFunction.html}, note=[Accessed: 17-November-2024 ]}