GreenFunction

GreenFunction[{ℒ[u[x]],ℬ[u[x]]},u,{x,xmin,xmax},y]

给出线性微分算子 ℒ 的 Green 函数，其中边界条件 ℬ 在范围 xmin 至 xmax 内.

GreenFunction[{ℒ[u[x1,x2,…]],ℬ[u[x1,x2,…]]},u,{x1,x2,…}∈Ω,{y1,y2,…}]

对区域 Ω 上的线性偏微分算子 ℒ 给出 Green 函数.

GreenFunction[{ℒ[u[x,t]],ℬ[u[x,t]]},u,{x,xmin,xmax},t,{y,τ}]

对于范围 xmin 到 xmax 内的线性时间相关算子 ℒ 给出 Green 函数.

GreenFunction[{ℒ[u[x1,…,t]],ℬ[u[x1,…,t]]},u,{x1,…}∈Ω,t,{y1,…,τ}]

给出区域 Ω 内线性时间相关算子 ℒ 的 Green 函数.

更多信息和选项

  • GreenFunction 表示冲击 DiracDelta 驱动函数的系统响应.
  • 微分算子 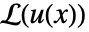的 GreenFunction 定义为 L(G(x;y))=TemplateBox[{{x, -, y}}, DiracDeltaSeq] 的解 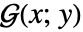，满足给定齐次边界条件 .
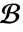  • 具有齐次边界条件 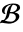的 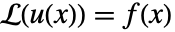的特定解可以通过执行卷积积分 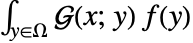得到.
  • 时间相关微分算子 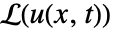的 GreenFunction 定义为 L(G(x,t;y,tau))=TemplateBox[{{x, -, y}}, DiracDeltaSeq]TemplateBox[{{t, -, tau}}, DiracDeltaSeq] 的解 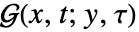，满足给定齐次边界条件 .
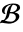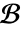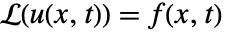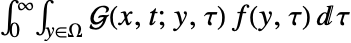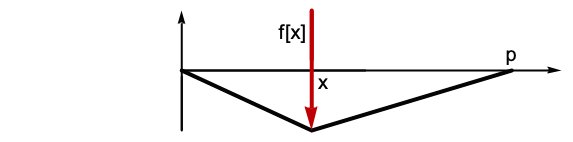
  • 具有齐次边界条件 的 的特解可以通过执行卷积积分 得到.
  • 典型偏微分方程的 Green 函数具有特征几何属性：
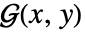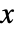  • 以关于 和 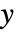的表达式给出，如果应变量的格式为 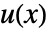，并且以正式参数 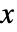和 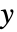的纯函数给出，如果应变量的格式为 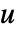而不是 . »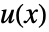
  • 区域 Ω 可以是满足 RegionQ[Ω] 为 True 的任何东西.
  • 常微分方程需要的初始条件和边界条件必须用 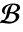指定.
  • 偏微分方程的边界条件必须在 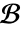中用 DirichletCondition 或者 NeumannValue 指定.
  • 参数上的假定应该使用 Assumptions 选项指定.

范例

打开所有单元关闭所有单元

基本范例  (2)

边值问题的 Green 函数：

实线上热算子的 Green 函数：

范围  (22)

基本用途  (2)

计算常微分算子的 Green 函数：

通过在第二个参数中使用 u 而不是 u[x] 在结果中获得纯函数：

计算偏微分算子的 Green 函数：

通过在第二个参数中使用 u 而不是 u[x,t] 获得结果中的纯函数：

常微分方程  (4)

计算初值问题的 Green 函数：

计算 Dirichlet 问题的 Green 函数：

计算纽曼问题的 Green 函数：

计算 Robin 问题的 Green 函数：

波动方程  (4)

实轴上波动算子的 Green 函数：

半线上具有 Dirichlet 条件的波动算子的 Green 函数：

半线内纽曼条件的波动算子的 Green 函数：

区间内具有 Dirichlet 条件的波动算子的 Green 函数：

热方程  (5)

实线上热算子的 Green 函数：

在半线上具有 Dirichlet 条件的热算子的 Green 函数：

区间内具有 Dirichlet 条件的热算子的 Green 函数：

在区间上具有纽曼条件的热算子的 Green 函数：

平面上热算子的 Green 函数：

拉普拉斯方程  (4)

二维空间内 Laplacian 的 Green 函数：

平面的象限的 Laplacian 的 Dirichlet 问题：

矩形内 Laplacian 的 Dirichlet 问题：

三维空间内 Laplacian 的 Green 函数：

Helmholtz 方程  (3)

二维空间内 Helmholtz 算子的 Green 函数：

上半平面内 Helmholtz 算子的 Dirichlet 问题：

矩形内 Helmholtz 算子的 Dirichlet 问题：

选项  (1)

Assumptions  (1)

指定 GreenFunction 中参数的 Assumptions：

在假定 t>s 下获得更简单的结果：

应用  (9)

常微分方程  (4)

使用 GreenFunction 求解非齐次微分方程的初始值问题：

定义力函数：

执行 Green 函数与力函数的卷积：

比较由 DSolveValue 给出的结果：

使用 GreenFunction 求解非齐次微分方程的 Dirichlet 问题：

定义力函数：

执行 Green 函数与力函数的卷积：

与由 DSolveValue 给出的结果比较：

使用 GreenFunction 求解非齐次微分方程的 Neumann 问题：

定义力函数：

执行 Green 函数与力函数的卷积：

与 DSolveValue 给出的结果进行比较：

使用 GreenFunction 求解非齐次微分方程的 Robin 问题：

定义力函数：

执行 Green 函数与力函数的卷积：

与由 DSolveValue 给出的结果比较:

偏微分方程  (2)

使用 GreenFunction 求解非齐次波动方程：

定义非齐次项：

使用 求解非齐次方程：

与由 DSolveValue 给出的解比较:

对使用 GreenFunction 的热方程求解初值问题：

指定初始值：

使用 求解初值问题：

与由 DSolveValue 给出的解比较：

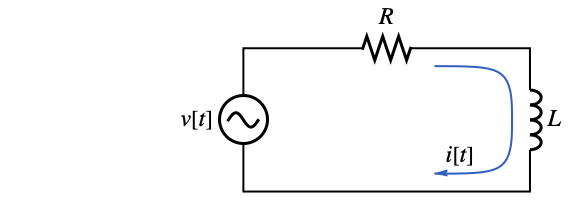
物理和工程  (3)

计算某电路的电流 i[t]，该电路的电压电源 v[t] 与电阻器 R 和电感器 L 相连. 该电路的算子由下式给出：

电路图：

计算 Green 函数：

求给定电压源的电流：

计算一条绳子的位移 u[x]，该绳子的长度为 p，张力为 T，两端被固定，并受到每单位长度 f[x] 的力. 该位移的算子由下式给出：

力图：

计算 Green 函数：

求给定力的位移：

连续线性时间恒定系统的冲击响应可用该系统的 Green 函数和齐次初始条件来计算. 计算按照下面式子定义的系统的冲击响应：

具有齐次初始条件的系统的 Green 函数：

通过设置 s=0 获得冲击响应：

绘制冲击响应的图线：

属性和关系  (2)

计算微分方程的 Green 函数：

使用 DSolve 获得相同结果：

GreenFunction 与 OutputResponse 和 TransferFunctionModel 相关：

Wolfram Research (2016)，GreenFunction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GreenFunction.html.

文本

Wolfram Research (2016)，GreenFunction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GreenFunction.html.

CMS

Wolfram 语言. 2016. "GreenFunction." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/GreenFunction.html.

APA

Wolfram 语言. (2016). GreenFunction. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GreenFunction.html 年

BibTeX

@misc{reference.wolfram_2024_greenfunction, author="Wolfram Research", title="{GreenFunction}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GreenFunction.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_greenfunction, organization={Wolfram Research}, title={GreenFunction}, year={2016}, url={https://reference.wolfram.com/language/ref/GreenFunction.html}, note=[Accessed: 17-November-2024 ]}