HadamardMatrix

HadamardMatrix[n]

返回一个 n×n 的阿达马 (Hadamard) 矩阵.

更多信息和选项

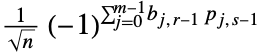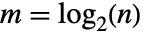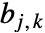  • 默认情况下，阿达马矩阵中的每一项 Hrs 的定义为 ，其中 ， 是整数 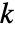的二进制表示的第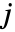 位，而 .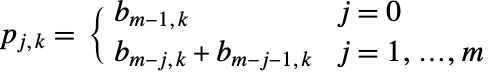
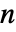  • 必须是 2 的幂.
  • HadamardMatrix 的行或列是 DiscreteHadamardTransform 的基序列.
  • Hadamard 矩阵是对称且正交的， 因此它的逆矩阵是自身. »
  • 支持下列选项：
  • Method Automatic指定序列排序方法
    WorkingPrecision ∞创建元素时使用的精度
  • Method 选项的设置指定了序列排序（阿达马基序列中的过零次数）. 可能的设置包括：
  • "BitComplement"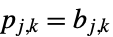
    "GrayCode"对 "BitComplement" 的格雷码重新排序
    "Sequency"顺序随行和列索引的增加而增加（默认）
  • 位补码排序也称为西尔维斯特（Sylvester）排序.
  • 序列排序也称为沃尔什（Walsh）排序.
  • 格雷码排序也称为二元排序（dyadic ordering）或帕利排序（Paley ordering）.
  • HadamardMatrix[…,TargetStructure…] 指定返回矩阵的结构. TargetStructure 的可能设置包括：
  • Automatic自动选择返回的表示
    "Dense"以稠密矩阵的形式表示矩阵
    "Hermitian"以埃尔米特矩阵的形式表示矩阵
    "Orthogonal"以正交矩阵的形式表示矩阵
    "Symmetric"以对称矩阵的形式表示矩阵
    "Unitary"以酉矩阵的形式表示矩阵
  • HadamardMatrix[…,TargetStructureAutomatic] 等价于 HadamardMatrix[…,TargetStructure"Dense"].

范例

打开所有单元关闭所有单元

基本范例  (1)

的阿达马矩阵：

长度为 128 的阿达马基本序列：

选项  (3)

Method  (1)

检测阿达马矩阵的行的序列值：

TargetStructure  (1)

以稠密矩阵的形式返回阿达马矩阵：

以对称矩阵的形式返回阿达马矩阵：

以正交矩阵的形式返回阿达马矩阵：

WorkingPrecision  (1)

默认情况下，计算精确矩阵：

使用机器精度：

使用任意精度：

属性和关系  (4)

向量的离散 Hadamard 变换等同于将向量乘以 Hadamard 矩阵：

4 阶 Hadamard 矩阵的 Sylvester 构造：

这对应于位补序列排序：

阿达马矩阵是对称且正交的：

由于这些属性，Hadamard 矩阵的逆矩阵是自身：

定义 n×n “位颠倒”置换矩阵，n 为 2 的幂：

定义 n×n 灰色编码置换矩阵，n 为 2 的幂：

生成具有不同序列排序的阿达马矩阵：

具有格雷码排序的阿达马矩阵等同于将格雷码排列应用于具有位补码序列置换的阿达马矩阵：

具有序列排序的阿达马矩阵等同于对具有格雷码排序的阿达马矩阵进行位颠倒置换：

带序列排序的阿达马矩阵等价于对带位补码序列排序的阿达马矩阵连续应用位颠倒置换和格雷码置换：

Wolfram Research (2012)，HadamardMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HadamardMatrix.html （更新于 2024 年）.

文本

Wolfram Research (2012)，HadamardMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HadamardMatrix.html （更新于 2024 年）.

CMS

Wolfram 语言. 2012. "HadamardMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/HadamardMatrix.html.

APA

Wolfram 语言. (2012). HadamardMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HadamardMatrix.html 年

BibTeX

@misc{reference.wolfram_2024_hadamardmatrix, author="Wolfram Research", title="{HadamardMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/HadamardMatrix.html}", note=[Accessed: 18-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hadamardmatrix, organization={Wolfram Research}, title={HadamardMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/HadamardMatrix.html}, note=[Accessed: 18-December-2024 ]}