HiddenMarkovProcess
HiddenMarkovProcess[i0,m,em]
遷移行列 m,放出行列 em,初期隠れ状態 i0の,離散時間,有限状態の隠れマルコフ(Markov)過程を表す.
HiddenMarkovProcess[…,m,{dist1,…}]
放出分布 distiの隠れマルコフ過程を表す.
HiddenMarkovProcess[p0,m,…]
初期隠れ状態確率ベクトル p0の,隠れマルコフ過程を表す.
詳細



- HiddenMarkovProcessは,隠れマルコフモデル(HMM)としても知られている.
- HiddenMarkovProcessは,離散時間・離散状態のランダム過程である.
- 隠れマルコフ過程は,もとになっている隠れ状態遷移過程としてDiscreteMarkovProcess[p0,m]を有する.放出と呼ばれる隠れマルコフ過程から観察された値はランダムで,状態 i において放出分布 distiに従う.指定された一連の状態を訪れている間に生成される放出は独立である.
- HiddenMarkovProcessの隠れ状態は,1から
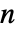 までの整数である.ただし,
までの整数である.ただし,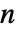 は遷移行列 m の長さである.
は遷移行列 m の長さである. - 遷移行列 m は,条件付きの隠れ状態遷移確率 m〚i,j〛Probability[x[k+1]jx[k]i]を指定する.ただし,x[k]は時点 k における過程の隠れ状態である.
- 放出行列 em は指定された隠れ状態 em〚i,r〛Probability[y[k]rx[k]i]における放出確率を指定する.ただし,x[k] は隠れ状態であり,y[k]は時点 k における放出である.
- 放出分布 distiはすべてが一変量あるいはすべてが多変量でなければならず,すべてが離散あるいはすべてが連続でなければならない.
- 放出分布 distiは,x[k]i であるならば y[k]distiであるように指定する.
- 放出を生成しない無音状態は,放出行列の場合は0の行で,一般放出の場合はNoneで表される.各無音状態は放出状態への経路を持たなければならない.
- 無音状態を持つ隠れマルコフ過程 proc については,HiddenMarkovProcess[proc]は無音状態を取り除いた有効な過程を与える.
- EstimatedProcess[data,HiddenMarkovProcess[n,edist]]を使い,edist で指定される族内の放出分布を持った n 状態過程を推定することができる.
- 次の特殊 edist テンプレートを使うことができる.
-
s s 回の離散放出 "Gaussian" ガウス放出 dist dist として分布されたすべての状態についての放出 {dist1,…,distn} 状態 i からの放出分布 disti - EstimatedProcessはProcessEstimatorについての次の設定を許容する.
-
Automatic パラメータ推定器を自動的に選ぶ "BaumWelch" 期待値を最大化することで対数尤度を最大化する "ViterbiTraining" もっとも確率の高い経路を復号化し,教師あり訓練を使う "StateClustering" クラスタリング,続いて教師あり訓練を使う "SupervisedTraining" 状態データと放出データの両方を使う推定 - "BaumWelch","ViterbiTraining","StateClustering"の各メソッドは推定において隠れ状態経路を指定する必要がないのに対し,"SupervisedTraining"は隠れ状態経路データへのアクセスがあることに依存する.
- LogLikelihood等のデータに対して使える関数は,Missing値を許容する.
- RandomFunction[HiddenMarkovProcess[…]]は,デフォルトで,放出のみを与える.Method->{"IncludeHiddenStates"->True}とすると,状態数列がメタデータとして含まれたTemporalDataオブジェクト td を与えるようになる.隠れ状態データは td["HiddenStates"]を使って取り出すことができる.
- HiddenMarkovProcessは,m が負の要素がなく行の合計が1の
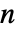 ×
× 行列であること,em が負の要素がなく行の合計が0か1の
行列であること,em が負の要素がなく行の合計が0か1の 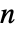 ×
×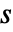 行列であること,i0が1から
行列であること,i0が1から 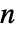 までの整数であること,p0が合計が1になる非負の要素の長さ
までの整数であること,p0が合計が1になる非負の要素の長さ 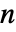 のベクトルであることを許容する.
のベクトルであることを許容する. - HiddenMarkovProcessは,LogLikelihood,FindHiddenMarkovStates,EstimatedProcess,PDF,Probability,RandomFunction等の関数で使うことができる.
例題
すべて開くすべて閉じるスコープ (17)
基本的な用法 (8)
放出数列のLogLikelihoodを計算する:
Noneあるいはゼロベクトルを使って無音状態を示す:
与えられた放出から,隠れ状態の最も可能性が高い数列を求める:
Noneを使って無音状態を示す:
Annotationによって注釈が付けられたGraphを使ってHiddenMarkovProcessを定義する:
推定 (5)
"BaumWelch"は,与えられた放出の尤度を反復的に最大にするデフォルトの推定器である:
"ViterbiTraining"は,指定された放出とそのもとになっている未知の状態の結合尤度を最大化する,反復的推定器である:
"StateClustering"は,高速ヒューリスティック非反復的推定を行うために,よく使われる:
"SupervisedTraining"は,与えられた放出と与えられた状態の結合尤度を最大化する推定器である:
"StateData"サブオプションを使い,与えられた放出のもとになっている状態に関するデータを指定する:
過程スライス特性 (4)
固定時点における放出分布のPDFを求める:
一般化と拡張 (1)
アプリケーション (11)
ゲーム (3)
ときに正直ではなくなるカジノがコインを賭けるゲームを提供しており,表が出る確率が裏が出る確率の3倍になる不正なコインを使う不正行為を働いている.カジノのディーラーは,不正なコインと公正なコインを10%の確率で秘密裏に交換していることが知られている:
どちらのコインで始めるかを同じ確率で想定した,結果の隠れマルコフ過程:
勝負を6回行うつもりだとして,少なくとも3回裏が出る確率を計算する:
一連の勝負で,カジノがどの回に不正なコインを使ったかを推測する:
赤,青,緑の色が付いた,たくさんのボールが入っている壷が3つある:
毎回,無作為に1つの壷を選び,ボールを選び,色を発表し,ボールを壷の1つに戻す.この過程が4回繰り返される.次の壷に移る確率は次の通りである:
各壷からある1色を取り出す確率は,各壷についての各ボール数の割合になる:
最初の壷を選ぶ与えられた確率についての隠れマルコフ過程を構築する:
ボールを{red,blue,green,green}の順で得る確率:
色の順序を与えられて,選ばれる確率が最も高い壷の順を求める:
一人称の視点でのシューティングゲームで,エージェントがある階に隠れており,プレーヤーに向かって飛び出す準備をしている.エージェントはプレーヤーを見ることはできないが,何をしているかを聞くことはでき,レイアウトの知識に照らしてプレーヤーの位置を推定することはできる.草,金属,水,ドアの4つのタイプの27の区域のレイアウトを考える:
プレーヤーが現在の区域に留まる確率は10%,隣接する区域のどれに移動するかの確率は等しい.ここから,次の遷移確率行列が与えられる:
遺伝学 (3)
DNA配列はACGTの4文字からなる.ヌクレオチド配列と呼ばれる部分配列は,異なる文字が出現する頻度で特徴付けられる.タスクの1つは,配列を異なるヌクレオチド配列に分割することである.エクソンから始まり,5'スプライス部位があり,イントロンで終る配列を与えられたとしよう.エクソンの塩基組成が一様なら,イントロンにはCおよびGが欠けており,スプライス部位のコンセンサスヌクレオチドは確率0.95でGであり,ヌクレオチドの頻度分布は以下の通りである:
状態マシンには,エクソン(1),スプライス(2),イントロン(3),終端(4)の状態があり,状態間には次の遷移確率がある:
放出は,ヌクレオチドA(1),C (2),G (3),T (4),終端(5)のいずれかである:
最も確率が高い現行のヌクレオチド配列(エクソン,スプライス,イントロン,終端)を求める:
BRCA1遺伝子の損傷した対立遺伝子Bによって遺伝した乳癌のリスクをモデル化する.それぞれの親遺伝子が確率1/2で各対立遺伝子に貢献しているとする:
母親が機能性の対立遺伝子ペア「bb」を持っており,息子が各対立遺伝子の組合せを持つ確率は以下の通りである:
息子の放出確率は,同じく男性である父親と等しい.放出は癌が1,癌ではないが2である:
二倍体植物の2遺伝子が,次の対立遺伝子があるものとして調べられている:
この植物は自殖性である.つまり,子孫の遺伝子型は親の遺伝子型のみに依存する:
DiscreteMarkovProcessを使って世代的な遺伝子型の変化をモデル化する:
対立遺伝子は植物の表現型,つまり可視の特徴を制御する.大文字対立遺伝子が対応する小文字の対立遺伝子に対して完全に優勢だと仮定する:
この植物の表現型(整数によって指標が付けられている)は隠れマルコフ過程でモデル化できる:
気象 (2)
その他 (2)
生産過程は,よい状態あるいは悪い状態のどちらかである.よい状態は90%の確率で持続する.一度状態が悪くなると,その状態は永遠に続く:
状態がよいときに,製品品質は99%の確率で許容範囲にある.状態が悪くなると,製品品質が許容範囲に入る確率は96%になる:
この過程が確率80%のよい状態から始まって,最初の製品が許容範囲内だとすると,次の2つの製品の品質が許容範囲内である確率は次の通りである:
可能な状態が00,01,10,11の,2ビットのレジスタについて考える.このレジスタは,同確率で,この4状態のいずれかから始まる:
各時間ステップで,レジスタはランダムに操作される.レジスタは1/2の確率で変化なしに置かれる.レジスタの2つのビットが逆になる確率は1/4で,右のビットが逆になる確率は1/4である:
特性と関係 (6)
離散放出のあるHiddenMarkovProcessのSliceDistributionは,評価すると経験的DataDistributionになる:
時点 ![]() と
と ![]() における放出の結合分布のPDFを求める:
における放出の結合分布のPDFを求める:
1回の指数放出のあるHiddenMarkovProcessの放出はHyperexponentialDistributionに従う:
一般的な放出分布に従うHiddenMarkovProcessの放出を評価するとMixtureDistributionになる:
放出行列として恒等式を持つ隠れマルコフモデルは,離散マルコフ過程と同等である:
HiddenMarkovProcessは,隠れ状態のラベル付け直しまで定義される:
テキスト
Wolfram Research (2014), HiddenMarkovProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html.
CMS
Wolfram Language. 2014. "HiddenMarkovProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html.
APA
Wolfram Language. (2014). HiddenMarkovProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html