HighpassFilter

HighpassFilter[data,ωc]

カットオフ周波数 ωcのハイパスフィルタをデータ配列に適用する．

HighpassFilter[data,ωc,n]

長さ n のフィルタカーネルを使う．

HighpassFilter[data,ωc,n,wfun]

平滑化窓 wfun をフィルタカーネルに適用する．

詳細とオプション

  • ハイパスフィルタリングは，通常，信号中の高周波数は変更せずに低周波数成分を減らすために使われる．
  • HighpassFilterは，窓法で作られた有限インパルス応答(FIR)カーネルでデジタル信号を変換する．
  • カットオフ周波数が大きいほど低周波数の損失が大きくなる．カーネルが長いほど，周波数の識別性が向上する．
  • data は以下のいずれでもよい．
  • list任意階数の数値配列
    tseriesTimeSeriesやTemporalDataのような時間データ
    image任意のImageオブジェクトまたはImage3Dオブジェクト
    audioAudioオブジェクトまたはSoundオブジェクト
  • 画像や多次元配列に適用された場合，フィルタリングはレベル1から始めて各次元に連続的に適用される．HighpassFilter[data,{ωc1,ωc2,…}]は 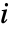次元で周波数 ωci を使う．
  • HighpassFilter[data,ωc]はカットオフ周波数 ωcと入力 data に適したフィルタカーネル長と平滑化窓を使う．
  • よく使われる平滑化窓 wfun
  • BlackmanWindowBlackman窓による平滑化
    DirichletWindow平滑化は行わない
    HammingWindowハミング窓による平滑化
    {v1,v2,…}値 viの窓を使う
    f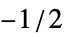から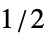の範囲で f をサンプリングして窓を作る
  • 使用可能なオプション
  • Padding "Fixed"使用する充填値
    SampleRate Automatic入力に想定されるサンプルレート
  • デフォルトで，リストと同様画像にもSampleRate->1が想定される．音声信号と時系列については，サンプルレートは抽出されるか入力データから計算されるかする．
  • SampleRatesr の場合，カットオフ周波数 ωcは 0から sr× 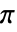まででなければならない．

例題

すべて開くすべて閉じる

例  (3)

正弦波数列にハイパスフィルタをかける：

Audioオブジェクトにハイパスフィルタをかける：

画像にハイパスフィルタをかける：

スコープ  (13)

データ  (8)

1Dパルス列にフィルタをかける：

2Dパルス列にフィルタをかける：

TimeSeriesにフィルタをかける：

スウェプトサイン（時間とともに周波数を変化させる正弦波）の音声信号にハイパスフィルタをかける：

デュアルトーン多重周波数(DTMF)信号のSoundオブジェクトにハイパスフィルタをかける：

2つの周波数の中間のカットオフ周波数，長さ101のフィルタ，Blackman窓を使う：

ハーフトーン画像のハイパスフィルタリング：

3D画像のハイパスフィルタリング：

厳密精度を使ったフィルタ：

パラメータ  (5)

音声信号の場合は，数値カットオフ周波数が1秒あたりのラジアンとして解釈される：

15000Hzのカットオフ周波数を使ってホワイトノイズ信号にフィルタをかける：

周波数の値をより低くする：

デフォルトで，フィルタの長さとその周波数弁別はカットオフ周波数に依存する：

より低い周波数にはより短いフィルタカーネルが使われる：

より長いカーネルを使って周波数弁別を向上させる：

窓関数を変えることでストップバンド減衰の量を変化させる：

調整可能なカイザー(Kaiser)窓を使って減衰の量を変える：

窓関数を数値リストとして指定する：

各次元に異なるカットオフ周波数を使う：

オプション  (3)

Padding  (1)

充填法を変えるとエッジ効果も変わる：

SampleRate  (2)

正規化されたサンプルレート sr=1を仮定して，長さ5のハーフバンドハイパスフィルタを使う：

サンプルレート sr=3を仮定する：

ハーフバンドハイパスフィルタをレートTemplateBox[{44100, "Hz", hertz, "Hertz"}, QuantityTF]でサンプリングされた音声に適用する：

アプリケーション  (3)

周期配列中のゼロ周波数成分を減らす：

HighpassFilterを使ってAudioオブジェクトの音が「より細く」なるようにする：

現代の88鍵のピアノでは，55番目のキー(C5)の基本周波数は約523Hzである．HighpassFilterを使って，以下の音声クリップにあるこのキーのすべての倍音を保持しつつ，基本波を効率的に削除する：

カットオフ周波数が基本周波数(523Hz)と最初の倍音(1046Hz)の中間にある長さ59のハイパスフィルタを使う：

2つの音声クリップの周波数スペクトルを比較する：

特性と関係  (8)

カットオフ周波数0を使うともとの列が返される：

π 以上のカットオフ周波数を使うとゼロの数列が返される：

LeastSquaresFilterKernelとHammingWindowを使ってハイパスフィルタを作る：

HighpassFilterの結果と比較する：

長さ21のハーフバンドハイパスフィルタのインパルス応答：

フィルタの振幅スペクトル：

平滑化窓なしでの長さ21のハーフバンドハイパスフィルタのインパルス応答：

フィルタの振幅スペクトル：

偶数長フィルタのインパルス応答：

フィルタの振幅スペクトル：

ハイパスフィルタの周波数弁別はフィルタの長さが長くなるにつれて向上する：

インパルス応答の長さはフィルタのバンド幅が減ずるにつれて長くなる：

考えられる問題  (1)

PaddingNoneを使うと出力の長さが入力よりも短くなる：

入力よりも長いカーネルを使うと空リストが返される：

Wolfram Research (2012), HighpassFilter, Wolfram言語関数， https://reference.wolfram.com/language/ref/HighpassFilter.html （2016年に更新）.

テキスト

Wolfram Research (2012), HighpassFilter, Wolfram言語関数， https://reference.wolfram.com/language/ref/HighpassFilter.html （2016年に更新）.

CMS

Wolfram Language. 2012. "HighpassFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/HighpassFilter.html.

APA

Wolfram Language. (2012). HighpassFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HighpassFilter.html

BibTeX

@misc{reference.wolfram_2024_highpassfilter, author="Wolfram Research", title="{HighpassFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/HighpassFilter.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_highpassfilter, organization={Wolfram Research}, title={HighpassFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/HighpassFilter.html}, note=[Accessed: 17-November-2024 ]}