Hyperplane

Hyperplane[n,p]

法線 n が点 p を通る超平面を表す．

Hyperplane[n,c]

を満足する点 で与えられる法線 n を持つ超平面を表す．

詳細

  • Hyperplaneは，幾何学空間およびグラフィックスプリミティブとして使うことができる．
  • Hyperplane[n]は，原点を通る超平面Hyperplane[n,0]に等しい．
  • Hyperplaneは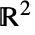，における無限直線および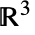における無限平面に相当する．
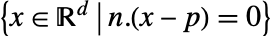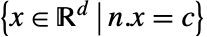  • Hyperplaneは，集合あるいはを表す．
  • Hyperplaneは，n∈d，p∈d，c∈について定義される．
  • Hyperplaneは，GraphicsおよびGraphics3Dで使うことができる．
  • Hyperplaneは，描画の際にPlotRangeで切り取られる．
  • Graphics描画は，Thickness，Dashing，Opacity等の指示子および色の影響を受ける．
  • Graphics3D描画は，Opacity等の指示子および色の影響を受ける．FaceForm[front,back]を使って front と back に別々のスタイルを指定することができる．ただし，front は法線 n の方向であると定義される．

例題

すべて開くすべて閉じる

例  (3)

2DのHyperplane：

3Dにおけるもの：

さまざまなスタイルを適用された超平面：

点が指定された超平面領域に属するかどうかを調べる：

スコープ  (15)

グラフィックス  (5)

指定  (2)

法線ベクトルと点で定義された2Dにおける超平面：

法線ベクトルと定数で定義された同じ超平面：

法線ベクトルと点を使って3Dの超平面を定義する：

法線ベクトルと定数を使って同じ超平面を定義する：

法線の方向が異なる超平面：

スタイル付け  (2)

色指示子で超平面の色を指定する：

FaceFormとEdgeFormを使って面と辺のスタイルを指定することができる：

座標  (1)

点とベクトルはDynamicでよい：

領域  (10)

埋込み次元は座標の次元である：

幾何学次元は領域そのものの次元である：

点の帰属判定：

帰属条件を得る：

超平面は無限測度と未定義の重心を持つ：

点からの距離：

点からの符号付き距離：

領域内の最近点：

最近点：

超平面は非有界である：

領域範囲を求める：

軸が揃っている場合は，ある方向については有界になる：

超平面上で積分する：

超平面上で最適化する：

超平面上で方程式を解く：

アプリケーション  (11)

超平面の揃え方  (7)

超平面を平行に並べると，すべての平面が同じ法線 n を持つようになる：

超平面を直交するように置く：

超平面の格子：

超平面をランダムに置く：

超平面の鉛筆はすべてが点を通る超平面である：

超平面の束はすべてが線を通る超平面である：

すべてが共通の点を通る超平面の塊：

接平面  (4)

2Dにおける陰的に定義された曲線 に対する接平面は，その法線TemplateBox[{{f, (, {x, ,, y}, )}, {{, {x, ,, y}, }}}, Grad]によって曲線上の点で与えられる．曲線上の点を求めることから始める：

各点における接線を求める：

解を可視化する：

3Dにおける陰的に定義された曲面 に対する接平面はその法線TemplateBox[{{f, (, {x, ,, y, ,, z}, )}, {{, {x, ,, y, ,, z}, }}}, Grad]と曲面上の点によって与えられる．曲面上の点を求めることから始める：

各点における接平面を求める：

解を可視化する：

パラメトリック曲線に対する接線は，パラメータ のなんらかの値についてその法線 fによって定義される．まず，パラメータの値を選ぶことから始める：

各パラメータ値についての接線を求める：

解を可視化する：

パラメトリック曲面に対する接平面は，パラメータ および のなんらかの値についてのその法線によって定義される．まず，パラメータの値を選ぶことから始める：

各点における接平面を求める：

解を可視化する：

特性と関係  (7)

HyperplaneはConicHullRegionの特殊ケースである：

HyperplaneはAffineSpaceの特殊ケースである：

InfiniteLineはHyperplaneの特殊ケースである：

InfinitePlaneはHyperplaneの特殊ケースである：

ParametricRegionは，における任意のHyperplaneを表すことができる：

における：

ImplicitRegionは，における任意のHyperplaneを表すことができる：

における：

指定されたについてのClipPlanesは，結果として，法線の負の方向に当たるの側には何も描画しないグラフィックスになる：

おもしろい例題  (4)

線のランダム集合：

平面のランダム集合：

線の組織化された集合：

軸の周りで超平面を回転させる：

Wolfram Research (2015), Hyperplane, Wolfram言語関数， https://reference.wolfram.com/language/ref/Hyperplane.html.

テキスト

Wolfram Research (2015), Hyperplane, Wolfram言語関数， https://reference.wolfram.com/language/ref/Hyperplane.html.

CMS

Wolfram Language. 2015. "Hyperplane." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Hyperplane.html.

APA

Wolfram Language. (2015). Hyperplane. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Hyperplane.html

BibTeX

@misc{reference.wolfram_2024_hyperplane, author="Wolfram Research", title="{Hyperplane}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/Hyperplane.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hyperplane, organization={Wolfram Research}, title={Hyperplane}, year={2015}, url={https://reference.wolfram.com/language/ref/Hyperplane.html}, note=[Accessed: 21-November-2024 ]}