InverseFourier

InverseFourier[list]

複素数のリストの離散逆フーリエ変換を求める．

InverseFourier[list,{p1,p2,…}]

指定の位置の離散逆フーリエ変換を返す．

詳細とオプション

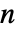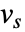  • 長さ のリスト に対する逆フーリエ変換 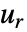は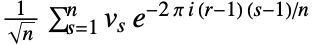，と定義される． »
  • 入力リストの1の位置に周波数ゼロの項が置かれなければならないことに注意．
  • 理工系の分野によっては他の定義が使われることもある．
  • 異なった定義の選択は，オプションFourierParametersを使用して指定できる．
  • FourierParameters->{a,b}の設定により，InverseFourierで計算される離散フーリエ変換は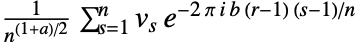となる．
  • よく使われる{a,b}として，{0,1}（デフォルト），{-1,1}（データ解析），{1,-1}（信号処理）がある．
  • b=-1と設定すると，事実上，入力および出力のリストを両方とも共役させることになる．
  • 離散フーリエ変換が一意的であるためには，Abs[b]は 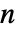と互いに素でなければならない．
  • このデータのリストの長さが2のベキである必要はない．
  • InverseFourier[list]の中の list は，任意の次元のデータの配列を表すためにネストさせることができる．
  • このデータの配列は矩形でなければならない．
  • InverseFourier[list,{p1,p2,…}]は，一般にExtract[InverseFourier[list],{p1,p2,…}]に等しい．位置が少ない場合，p は，メモリ量や時間は少なくて済むが，数値誤差の影響を（特に list が長い場合に）受けやすいアルゴリズムを使って計算される．
  • list にある要素が厳密な数である場合，InverseFourierは，まずこの要素にNを適用する．

例題

すべて開くすべて閉じる

例  (2)

実数リストの逆フーリエ変換：

複素数のリストの逆フーリエ変換：

スコープ  (3)

x は実数値のリストである：

機械演算で逆フーリエ変換を計算する：

24桁精度演算で計算する：

2D逆フーリエ変換を計算する：

x は1つの非零項を持った階数4のテンソルである：

4D逆フーリエ変換を計算する：

オプション  (3)

FourierParameters  (3)

正規化は行わない：

で正規化する：

で正規化する：

InverseFourierはパラメータ のFourierに等しい：

ノイズのあるシンク関数からのデータ：

フーリエ変換を得る：

スペクトルの一部から信号を再構築する：

アプリケーション  (1)

ガウスのデータ：

各モードを乗算して一次導関数を得る：

データの一次導関数を近似する：

導関数の近似は陰的に周期性を仮定することに注意：

特性と関係  (2)

はで与えられる：

InverseFourierは，指定のパラメータを使ってのFourierMatrixによる乗算に等しい：

行列の共役転置はFourierに等しい：

考えられる問題  (1)

InverseFourierは，少数の係数のみが必要な場合は，効率のよいアルゴリズムを使う：

高速で効率のよい実装は，重大な数値誤差を生じかねない：

Wolfram Research (1988), InverseFourier, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseFourier.html （2012年に更新）.

テキスト

Wolfram Research (1988), InverseFourier, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseFourier.html （2012年に更新）.

CMS

Wolfram Language. 1988. "InverseFourier." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/InverseFourier.html.

APA

Wolfram Language. (1988). InverseFourier. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseFourier.html

BibTeX

@misc{reference.wolfram_2024_inversefourier, author="Wolfram Research", title="{InverseFourier}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/InverseFourier.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inversefourier, organization={Wolfram Research}, title={InverseFourier}, year={2012}, url={https://reference.wolfram.com/language/ref/InverseFourier.html}, note=[Accessed: 17-November-2024 ]}