InverseTransformedRegion

InverseTransformedRegion[reg,f,n]

逆変換された領域を表す．ただし，reg は領域であり f は関数である．

詳細とオプション

例題

すべて開くすべて閉じる

例  (2)

回転された矩形の逆変換：

からの円板の逆像：

スコープ  (22)

特別な領域  (9)

逆変換された領域の中には明示的に計算できるものがある：

変換を可視化する：

線形分数変換による単位直方体の逆画像：

変換を可視化する：

平行移動された単位Diskの逆変換：

これを可視化する：

せん断された単位Rectangleの逆変換：

これを可視化する：

回転されたTriangleの逆変換：

これを可視化する：

スケールされたCircleの逆変換：

単位立方体の回転変換を介した逆画像：

これを可視化する：

線形変換による長方形の逆変換：

これを可視化する：

2Dに埋込まれたTriangleからの点を，非線形変換で3Dにマップする：

これを可視化する：

数式定義領域  (4)

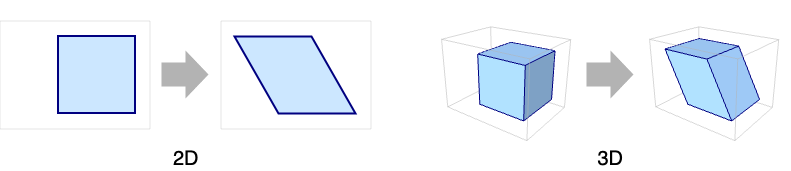
せん断されたParametricRegionの逆変換：

これを可視化する：

回転されたParametricRegionの逆変換：

これを可視化する：

せん断されたImplicitRegionの逆変換：

これを可視化する：

スケールされたImplicitRegionの逆変換：

これを可視化する：

メッシュ領域  (2)

BoundaryMeshRegionオブジェクトを逆変換したものはBoundaryMeshRegionである：

2D：

3D：

MeshRegionオブジェクトを逆変換したものはMeshRegionである：

2D：

3D：

派生領域  (5)

反射されたTransformedRegionの逆変換：

これを可視化する：

回転されたRegionDifferenceの逆変換：

これを可視化する：

スケールされたRegionBoundaryの逆変換：

これを可視化する：

反射されたRegionProductの逆変換：

これを可視化する：

非線形変換によるRegionUnionの逆変換：

これを可視化する：

地理的領域  (2)

InverseTransformedRegionは地理実体の多角形に使うことができる：

GeoPositionを使った多角形：

GeoPositionXYZを使った多角形：

GeoPositionENUを使った多角形：

GeoGridPositionを使った多角形：

Wolfram Research (2014), InverseTransformedRegion, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseTransformedRegion.html.

テキスト

Wolfram Research (2014), InverseTransformedRegion, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseTransformedRegion.html.

CMS

Wolfram Language. 2014. "InverseTransformedRegion." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseTransformedRegion.html.

APA

Wolfram Language. (2014). InverseTransformedRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseTransformedRegion.html

BibTeX

@misc{reference.wolfram_2024_inversetransformedregion, author="Wolfram Research", title="{InverseTransformedRegion}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/InverseTransformedRegion.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inversetransformedregion, organization={Wolfram Research}, title={InverseTransformedRegion}, year={2014}, url={https://reference.wolfram.com/language/ref/InverseTransformedRegion.html}, note=[Accessed: 21-November-2024 ]}