KolmogorovSmirnovTest
KolmogorovSmirnovTest[data]
使用 Kolmogorov-Smirnov 检验判断 data 是否服从正态分布.
KolmogorovSmirnovTest[data,dist]
使用 Kolmogorov-Smirnov 检验判断 data 是否服从 dist 分布.
KolmogorovSmirnovTest[data,dist,"property"]
返回 "property" 的值.
更多信息和选项



- KolmogorovSmirnovTest 执行 Kolmogorov–Smirnov 拟合优度检验,其中零假设
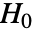 为 data 抽取自分布为 dist 的总体,而备择假设
为 data 抽取自分布为 dist 的总体,而备择假设 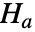 认为并非如此.
认为并非如此. - 默认情况下,返回一个概率值或者
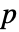 值.
值. - 一个较小的
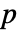 值表明 data 不可能服从 dist.
值表明 data 不可能服从 dist. - dist 可以是任意具有数值和符号参数或者数据集的符号分布.
- data 可以是单变量 {x1,x2,…} 或者多变量 {{x1,y1,…},{x2,y2,…},…}.
- Kolmogorov-Smirnov 检验假设数据来自一个连续分布.
- Kolmogorov-Smirnov 检验实际上使用基于
![sup_x TemplateBox[{{{{F, ^, ^}, (, x, )}, -, {F, (, x, )}}}, Abs] sup_x TemplateBox[{{{{F, ^, ^}, (, x, )}, -, {F, (, x, )}}}, Abs]](Files/KolmogorovSmirnovTest.zh/5.png) 的检验统计量,其中
的检验统计量,其中 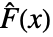 是 data 的经验 CDF,而
是 data 的经验 CDF,而 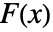 是 dist 的 CDF.
是 dist 的 CDF. - 对于多变量检验,使用单变量边缘检验的
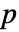 的和,并且在
的和,并且在 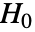 下假定服从 UniformSumDistribution.
下假定服从 UniformSumDistribution. - KolmogorovSmirnovTest[data,dist,"HypothesisTestData"] 返回一个 HypothesisTestData 对象 htd,通过使用htd["property"] 的形式,它可以用来提取额外的检验结果和属性.
- KolmogorovSmirnovTest[data,dist,"property"] 可以用来直接给出 "property" 的值.
- 与检验结果的报告相关的属性包括:
-
"PValue" 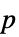 值
值"PValueTable" "PValue" 的格式化版本 "ShortTestConclusion" 一个检验结论的简短描述 "TestConclusion" 一个检验结论的描述 "TestData" 检验统计量和 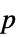 值
值"TestDataTable" "TestData" 的格式化版本 "TestStatistic" 检验统计量 "TestStatisticTable" 格式化的 "TestStatistic" - 下列属性与所执行的检验类型无关.
- 与数据分布相关的属性包括:
-
"FittedDistribution" 数据的拟合分布 "FittedDistributionParameters" 数据的分布参数 - 可以给出下列选项:
-
Method Automatic 计算 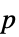 -值所用的方法
-值所用的方法SignificanceLevel 0.05 诊断和报告的分界点 - 对于一个拟合优度检验,选择一个临界值
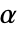 ,以使得只有当
,以使得只有当 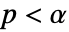 时,否定
时,否定 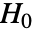 . 用于 "TestConclusion" 和 "ShortTestConclusion" 属性的
. 用于 "TestConclusion" 和 "ShortTestConclusion" 属性的 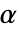 值由 SignificanceLevel 选项控制. 默认情况下,
值由 SignificanceLevel 选项控制. 默认情况下,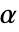 设为 0.05.
设为 0.05. - 在设置 Method->"MonteCarlo" 下,在
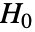 下使用拟合分布,生成
下使用拟合分布,生成 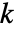 个与输入
个与输入 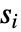 具有相同长度的数据集. 来自KolmogorovSmirnovTest[si,dist,"TestStatistic"] 的 EmpiricalDistribution 用于估计
具有相同长度的数据集. 来自KolmogorovSmirnovTest[si,dist,"TestStatistic"] 的 EmpiricalDistribution 用于估计 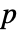 值.
值.
范例
打开所有单元关闭所有单元范围 (9)
检验 (6)
执行 Kolmogorov-Smirnov 检验对正态性进行校验:
创建一个 HypothesisTestData 对象以进行重复属性提取:
选项 (4)
应用 (2)
对功效曲线进行 Kolmogorov-Smirnov 检验:
当内在分布是一个 UniformDistribution[{-4,4}],检验尺度为0.05,样本数为 12 时,估计Kolmogorov-Smirnov 检验的功效:
31片飞机玻璃样品可以承受一定的压力直至断裂为止. 调查数据是否从一个 NormalDistribution 或者一个 GammaDistribution 抽取:
比较候选分布的分位数图线(Quantile-Quantile plot):
相对于 NormalDistribution,数据使用 GammaDistribution 的拟合程度稍微好些:
属性和关系 (9)
默认情况下,单变量数据与 NormalDistribution 相比较:
默认情况下,多变量数据与 MultinormalDistribution 相比较:
如果参数未知,则当可能的情况下,KolmogorovSmirnovTest 应用一次校正:
在执行典型的 Kolmogorov-Smirnov 检验之前估计参数:
从概念上讲,Kolmogorov-Smirnov 检验计算经验和理论 CDFs 的最大绝对差值:
当输入为 TimeSeries 时,Kolmogorov–Smirnov 检验只适用于数值:
可能存在的问题 (3)
Kolmogorov–Smirnov 检验不适用于离散分布:
在这些情况下,使用蒙特卡洛方法或者 PearsonChiSquareTest:
当参数已经从数据中估计得到时,对于某些分布,Kolmogorov-Smirnov 检验是无效的:
文本
Wolfram Research (2010),KolmogorovSmirnovTest,Wolfram 语言函数,https://reference.wolfram.com/language/ref/KolmogorovSmirnovTest.html.
CMS
Wolfram 语言. 2010. "KolmogorovSmirnovTest." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/KolmogorovSmirnovTest.html.
APA
Wolfram 语言. (2010). KolmogorovSmirnovTest. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/KolmogorovSmirnovTest.html 年