LowerTriangularMatrix

LowerTriangularMatrix[lmat]

下三角行列 lmat を構造化配列として表す．

詳細とオプション

  • 下三角行列は，構造化配列として表されているときは，Det，Inverse，LinearSolve等における効率的な保存とより効率的な操作を可能にする．
  • 下三角行列は，前進置換で解ける簡単な系を表す線型方程式系を解く際に出現する．上三角行列および下三角行列を使う行列分解には，LU，LDL， LL ((コレスキー分解) およびLQの各分解がある．
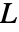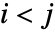  • 下三角行列 は のとき 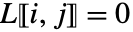を満足する．
  • 要素 lijは数値ではなくてもよい．
  • 下三角行列の逆行列は別の下三角行列である．
  • 下三角行列は行列の乗算のもとで閉じているので 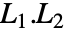もまた下三角行列である．
  • 下三角行列の行列式は対角要素 の積で与えられる．
  • LowerTriangularMatrixで高速化される操作には以下がある．
  • Det時間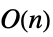
    Dot時間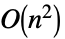
    LinearSolve時間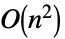
  • LowerTriangularMatrix sa については sa["prop"]で特性"prop"にアクセスできる．
  • "Matrix"完全な配列として表された下三角行列
    "Properties"サポートされる特性のリスト
    "Structure"構造化配列の型
    "StructuredData"構造化配列に保存された内部データ
    "StructuredAlgorithms"構造化配列についての特別なメソッドを持つ関数のリスト
    "Summary"Datasetとして表された情報のまとめ
  • Normal[LowerTriangularMatrix[…]]は下三角行列を通常の行列として与える．
  • LowerTriangularMatrix[…,TargetStructure->struct]は下三角行列を struct で指定された形式で返す．次は，その可能な設定である．
  • Automatic返す表現を自動選択する
    "Dense"行列を密な行列として表す
    "Sparse"行列を疎な配列として表す
    "Structured"行列を構造化配列として表す
  • LowerTriangularMatrix[…,TargetStructureAutomatic]はLowerTriangularMatrix[…,TargetStructure"Structured"]に等しい．

例題

すべて開くすべて閉じる

例  (2)

下三角行列を構築する：

要素を示す：

NormalはLowerTriangularMatrixをその通常表現に変換できる：

下三角行列を記号成分で構築する：

要素を示す：

行列式を得る：

スコープ  (5)

LowerTriangularMatrixオブジェクトは行列についての情報を与える特性を含む：

"Summary"特性は行列についての情報の簡単なまとめを与える：

"StructuredAlgorithms"特性は表現の構造を使うアルゴリズムを持つ関数のリストを与える：

構造化アルゴリズムの方が通常は速い：

行列式を計算する：

逆行列を計算する：

線形系を解く：

固有値を計算する：

構造化アルゴリズムは，適切な場合は別のLowerTriangularMatrixオブジェクトを返す：

ltの逆行列は別の下三角行列である：

ltの転置は上三角行列を与える：

ltとその転置の積はもはや三角行列ではない：

整数成分を持つSparseArrayから下三角行列を構築する：

要素を示す：

複素数値の下三角行列を構築する：

行列式を計算する：

逆行列を計算する：

線形系を解く：

固有値を計算する：

オプション  (1)

TargetStructure  (1)

下三角行列を密な行列として返す：

下三角行列を構造化配列として返す：

下三角行列を疎な配列として返す：

アプリケーション  (2)

行列のLU分解を計算するための関数：

分解を計算する：

分解を確かめる：

2つの n×n 行列：

2つの行列をブロックとして持つ3n×3n 単位下三角行列を構築する：

逆行列の n×n 下左部分行列はもとの2つの行列の積に等しい：

特性と関係  (2)

LowerTriangularMatrixはUpperTriangularMatrixを与える：

LowerTriangularMatrixの成分は最も低い精度にされる：

考えられる問題  (1)

全行列：

LowerTriangularMatrix[a]は，a が明らかに下三角行列でなければ評価されない：

LowerTriangularMatrix[LowerTriangularize[a]]を使って a の下三角部分を得る：

おもしろい例題  (2)

第1種スターリング(Stirling)行列：

第2種スターリング行列：

2種類のスターリング行列は互いに互いの逆行列である：

次は，列の符号が交代するパスカル(Pascal)行列の変形である：

これが対合行列である（二乗すると恒等行列になる）ことを確認する：

Wolfram Research (2022), LowerTriangularMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html （2023年に更新）.

テキスト

Wolfram Research (2022), LowerTriangularMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html （2023年に更新）.

CMS

Wolfram Language. 2022. "LowerTriangularMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html.

APA

Wolfram Language. (2022). LowerTriangularMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html

BibTeX

@misc{reference.wolfram_2024_lowertriangularmatrix, author="Wolfram Research", title="{LowerTriangularMatrix}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_lowertriangularmatrix, organization={Wolfram Research}, title={LowerTriangularMatrix}, year={2023}, url={https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html}, note=[Accessed: 21-November-2024 ]}