MaternPointProcess

MaternPointProcess[μ,λ,rm,d]

represents a Matérn cluster point process with density μ, cluster mean λ and radius rm in .

Details

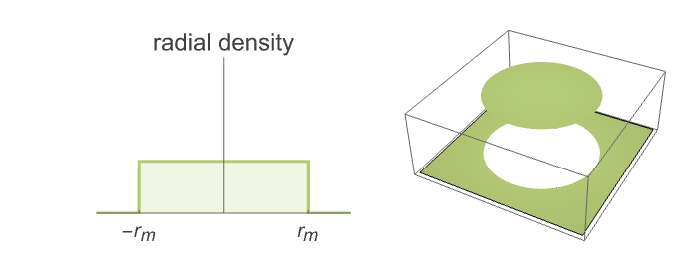
  • MaternPointProcess models clustered point configurations with cluster centers uniformly distributed over space and cluster points isotropically distributed with a uniform radial distribution.
  •     
  • Typical uses include things like plants or trees as centers with seedlings as the points of the cluster.
  • The cluster centers are placed according to PoissonPointProcess with density μ.
  • The point count of a cluster is distributed according to PoissonDistribution with mean λ.
  • The cluster points are uniformly distributed in a ball of radius rm around the cluster center.
  •     
  • MaternPointProcess allows μ, λ and rm to be any positive real numbers and d to be any positive integer.
  • The following settings can be used for PointProcessEstimator for estimating MaternPointProcess:
  • "FindClusters"use FindClusters function
    "MethodOfMoments"use a homogeneity measure to estimate the parameters
  • MaternPointProcess can be used with such functions as RipleyK, PointCountDistribution and RandomPointConfiguration.

Examples

open allclose all

Basic Examples  (3)

Sample from a Matérn point process over a unit disk:

Sample from a Matérn point process over a unit ball:

Sample from a Matérn point process over a geo region:

Scope  (3)

Sample from a valid region whose dimension is equal to its embedding dimension:

Check the region conditions:

Sample from a Matérn point process in the region and visualize the points:

Simulate a point configuration from a Matérn point process:

Use the "FindClusters" method to estimate a point process model:

Compare the Ripley measure between the original process and the estimated model:

Pair correlation function of a Matérn point process:

Visualize the function with given parameter values:

Properties & Relations  (5)

PointCountDistribution is known:

Mean and variance:

Plot the PDF:

Simulate the distribution:

The probability density histogram:

Ripley's and Besag's for Matérn point process in 2D:

Ripley's of Matérn point process is larger than for a Poisson point process:

Compare to the Poisson point process:

Besag's of Matérn point process is larger than for a Poisson point process:

Compare to the Poisson point process:

Pair correlation of Matérn point process is larger than 1:

Compare to homogeneous Poisson point process:

Possible Issues  (1)

The estimation algorithm splitting the point data into clusters may find a different cluster radius than in a model used to create a given point collection:

Estimate all the parameters:

Therefore, specifying a smaller cluster radius than is inferred from the data will result in the failure of finding a point process model:

Wolfram Research (2020), MaternPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/MaternPointProcess.html.

Text

Wolfram Research (2020), MaternPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/MaternPointProcess.html.

CMS

Wolfram Language. 2020. "MaternPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MaternPointProcess.html.

APA

Wolfram Language. (2020). MaternPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MaternPointProcess.html

BibTeX

@misc{reference.wolfram_2024_maternpointprocess, author="Wolfram Research", title="{MaternPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/MaternPointProcess.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_maternpointprocess, organization={Wolfram Research}, title={MaternPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/MaternPointProcess.html}, note=[Accessed: 21-November-2024 ]}