VarianceGammaPointProcess[μ,λ,α,β,d]
represents a variance gamma cluster point process with density μ, cluster mean λ and shape parameters α and β in ![]() .
.


VarianceGammaPointProcess
VarianceGammaPointProcess[μ,λ,α,β,d]
represents a variance gamma cluster point process with density μ, cluster mean λ and shape parameters α and β in ![]() .
.
Details

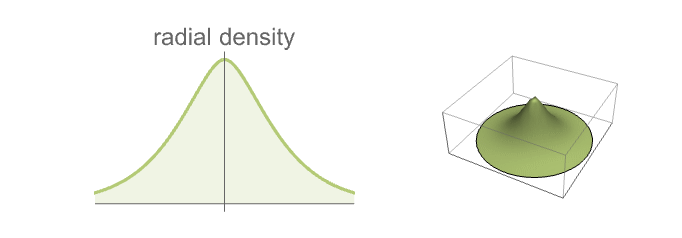
- VarianceGammaPointProcess models clustered point configurations with centers uniformly distributed over space and cluster points isotropically distributed with a flexible radial distribution.
- Typical uses include cosmology and rainforest tree distribution.
- The cluster centers are placed according to PoissonPointProcess with density μ.
- The point count of a cluster is distributed according to PoissonDistribution with mean λ.
- The cluster points in each cluster in
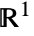 are distributed according to VarianceGammaDistribution[α,
are distributed according to VarianceGammaDistribution[α,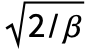 ,0,0].
,0,0]. - The cluster points in
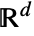 are distributed according to MultinormalDistribution[DiagonalMatrix[{u,u,…}]], with
are distributed according to MultinormalDistribution[DiagonalMatrix[{u,u,…}]], with 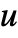 sampled from GammaDistribution[α,β] centered at a cluster center.
sampled from GammaDistribution[α,β] centered at a cluster center. - VarianceGammaPointProcess allows μ, λ, α and β to be any positive real numbers, and d to be any positive integer.
- The following settings can be used for PointProcessEstimator for estimating VarianceGammaPointProcess:
-
"FindClusters" use FindClusters function "MethodOfMoments" use a homogeneity measure to estimate the parameters - VarianceGammaPointProcess can be used with such functions as RipleyK, PointCountDistribution and RandomPointConfiguration.

Examples
open all close allBasic Examples (4)
Scope (2)
Sample from any valid RegionQ, whose RegionEmbeddingDimension is equal to its RegionDimension:
Simulate a point configuration from a variance gamma point process:
Use the "FindClusters" method to estimated a point process model:
Compare Ripley's ![]() measure between the original process and the estimated model:
measure between the original process and the estimated model:
Properties & Relations (5)
The PointCountDistribution is known:
The probability density histogram:
Ripley's ![]() and Besag's
and Besag's ![]() for a variance gamma point process in 2D:
for a variance gamma point process in 2D:
Ripley's ![]() of a variance gamma point process is larger than for a Poisson point process:
of a variance gamma point process is larger than for a Poisson point process:
Compare to a Poisson point process:
Besag's ![]() of a variance gamma point process is larger than for a Poisson point process:
of a variance gamma point process is larger than for a Poisson point process:
Compare to a Poisson point process:
The pair correlation of a variance gamma point process is larger than 1:
Related Guides
History
Text
Wolfram Research (2020), VarianceGammaPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/VarianceGammaPointProcess.html.
CMS
Wolfram Language. 2020. "VarianceGammaPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VarianceGammaPointProcess.html.
APA
Wolfram Language. (2020). VarianceGammaPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VarianceGammaPointProcess.html
BibTeX
@misc{reference.wolfram_2025_variancegammapointprocess, author="Wolfram Research", title="{VarianceGammaPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/VarianceGammaPointProcess.html}", note=[Accessed: 15-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_variancegammapointprocess, organization={Wolfram Research}, title={VarianceGammaPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/VarianceGammaPointProcess.html}, note=[Accessed: 15-January-2026]}