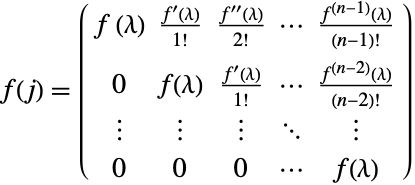MatrixFunction
MatrixFunction[f,m]
行列の引数 m でスカラー関数 f によって生成された行列を与える.
詳細とオプション

- 行列関数は行列を異なる行列に変換する.収束ベキ級数の場合,MatrixFunction[f,m]は,事実上,通常のベキを行列ベキで置き換えて関数 f についてのベキ級数を評価する. »
- 関数 f は一変数で微分可能であるか,さもなければ記号関数でなければならない.
- MatrixFunctionは正方行列にのみ使うことができる.これは,非厳密行列にはシューア・パーレット(Schur–Parlett) メソッドを,厳密行列あるいは記号行列にはジョルダン(Jordan)分解を適用する.
- MatrixFunctionはSparseArrayオブジェクトおよび構造化配列に使うこともできる.
- 場合によっては明示的な設定を含むMethodオプションを与えることができる.
-
"Jordan" ジョルダン分解 "Schur" ブロックパーレット反復を伴うシューア分解 - "Schur"メソッドはメソッドオプション mopts を使って Method{"Schur", mopts}とすることで指定できる.次は使用可能なメソッドオプションである.
-
"Balanced" False シューア分解の前に入力行列を平衡させるかどうか "BlockSeparationDelta" Automatic 単一のパーレットブロック内の隣接固有値間の最大距離
例題
すべて開くすべて閉じる例 (3)
スコープ (11)
基本的な用法 (7)
特殊行列 (4)
より一般的には,任意の対角行列の関数はその対角要素に適用された関数である:
HilbertMatrixの平方を20桁精度で計算する:
オプション (4)
アプリケーション (5)
特性と関係 (11)
関数![]() &を使うのはInverseを使うのに等しい:
&を使うのはInverseを使うのに等しい:
ベキである関数を使うのはMatrixPowerを使うのに等しい:
MatrixFunction[Exp,m]は基本的にMatrixExp[m]に等しい:
MatrixFunctionは,事実上,PowerをMatrixPowerに置き換えてベキ級数を使う:
![]() であるようにMatrixExp[MatrixFunction[Log,m]]は m に等しい:
であるようにMatrixExp[MatrixFunction[Log,m]]は m に等しい:
m が対角行列なら,MatrixFunction[f,m]は単に f を m の対角の各要素に適用するに過ぎない:
m が上三角行列なら,MatrixFunction[f,m]もまた上三角行列である:
![]() はJordanDecomposition
はJordanDecomposition ![]() によって
によって ![]() として計算できる:
として計算できる:
考えられる問題 (4)
スカラー関数は厳密行列あるいは記号行列について記号導関数を持つことができる:
MatrixFunctionはAbsのように微分不可能な関数には使えない:
これは,厳密な入力行列に対しては行列関数を返すが,Absには一次導関数も二次導関数もないので結果は無意味である:
MatrixFunctionはスカラー関数あるいはその任意の最初の導関数が行列固有値で定義されていない場合は結果を返さない:
スカラー関数が分析的ではなく行列の固有値が関数の極に近い場合,結果の行列は大抵の場合正しくない:
おもしろい例題 (1)
テキスト
Wolfram Research (2012), MatrixFunction, Wolfram言語関数, https://reference.wolfram.com/language/ref/MatrixFunction.html (2014年に更新).
CMS
Wolfram Language. 2012. "MatrixFunction." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/MatrixFunction.html.
APA
Wolfram Language. (2012). MatrixFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixFunction.html