MatrixGamePlot[mgame]
MatrixGame mgame のプロットを生成する.
MatrixGamePlot[mgame,strat]
ゲーム戦略 strat をハイライトする.


MatrixGamePlot
MatrixGamePlot[mgame]
MatrixGame mgame のプロットを生成する.
MatrixGamePlot[mgame,strat]
ゲーム戦略 strat をハイライトする.
詳細とオプション




- MatrixGamePlotは,通常,行列ゲームとのやり取りとその理解のために使われる.
- 2人ゲームには利得ベクトルの行列がある.各ベクトルは各プレーヤーの利得を表す.
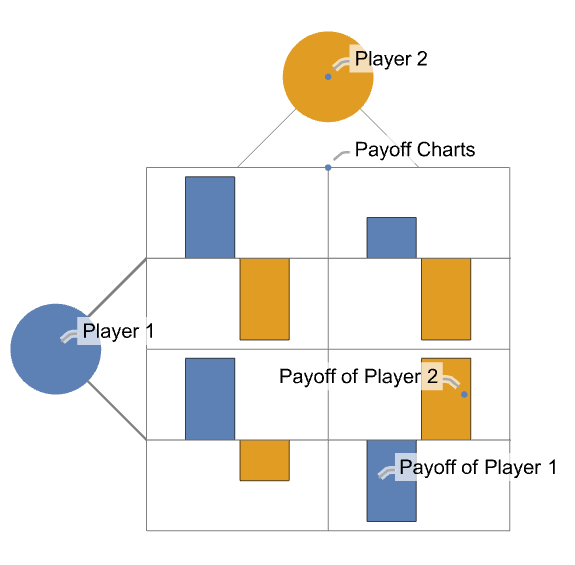
- 次のプロットはプレーヤーが2人のゲームである.利得はグラフとしてプロットされており,プレーヤーに関連付けられた色で彩色されている.
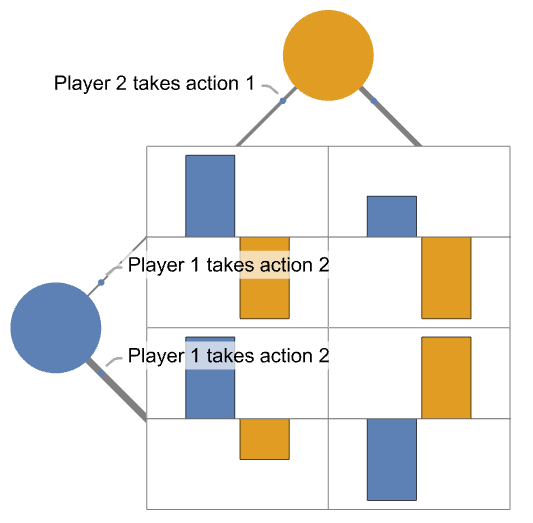
- 戦略も各プレーヤーの行と列の線の太さとして表すことができる.プレーヤーの行動の順序は上から下,左から右である.
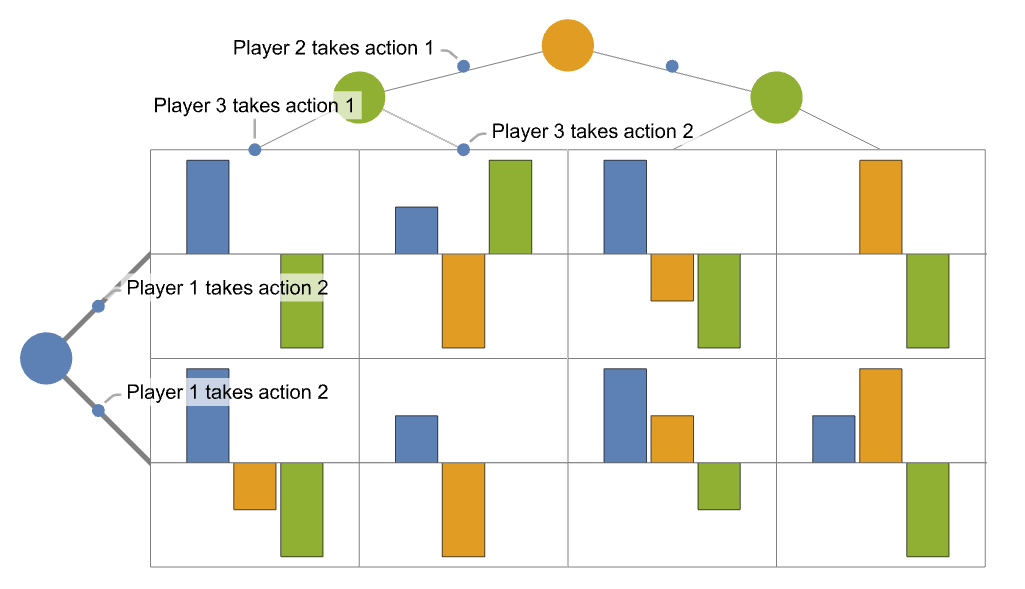
- 行または列に複数のプレーヤーがいる場合,プレーヤーの行動の各組合せに行または列が使われる.
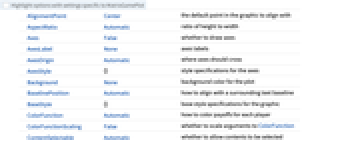
- MatrixGamePlotにはGraphicsと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
ColorFunction Automatic 各プレーヤーの利得の彩色方法 ColorFunctionScaling False ColorFunctionの引数をスケールするかどうか GameActionLabels Automatic 行動に使うラベル GamePlayerLabels Automatic プレーヤーに使うラベル PlotLayout Automatic 矩形と行のレイアウトを指定する PlotLegends Automatic 利得値の凡例 - ColorData["DefaultPlotColors"]は,ColorFunctionで使われるデフォルトの色のシーケンスを与える.
- 次は,PlotLayoutの可能な設定である.
-
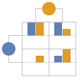
"BarChart" 各利得の矩形をBarChartとしてプロットする 
"SplitSquare" 各利得の矩形を分割矩形としてプロットする 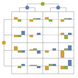
{{r1,…,rk},{c1,…,cn-k}} 行のプレーヤーと列のプレーヤーを変更する 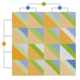
{"SplitSquare",{{…},{…}}} 前の2つのオプションを組み合せる - 利得配列は,プレーヤー{r1,…,rk}を行プレーヤー,{c1,…,cn-k}を列プレーヤーとする行列になるように再形成される可能性がある点に注意のこと.例えばプレーヤーが5人いる場合,デフォルトの順序では,最初の2人のプレーヤー({1,2}) が行に,他の3人のプレーヤー({3,4,5})が列に分割される.この順序はこのオプションを使用して変更できる.
全オプションのリスト


例題
すべて開く すべて閉じる例 (4)
GameActionLabels配列と同じ次元の配列を使って戦略を表示する:
スコープ (5)
オプション (6)
ColorFunction (1)
ColorDataに見られるようにカラースキームを指定する:
PlotLayout (1)
アプリケーション (9)
娯楽ゲーム (2)
社会ゲーム (1)
囚人のジレンマ (2)
経済ゲーム (3)
腹を空かせた3人の男がレストランに行き,割り勘にすることにした.店には,安い,中間,高いの3種類の定食がある.この状況をMatrixGameとして表す:
Cournot寡占ゲームは,一組の企業が同じ製品を生産している状況を表している.各企業が生産コストと他の企業の製品品質を考慮しなければならない.最低価格の企業だけが製品を販売することができる.
直感的に,すべてのプレーヤーを考慮した際に,2番目の行動の利得が最大であることが分かる:
価格戦争は,複数の企業が最低価格の製品を提供しようとしている状況を表している.企業の利得は選択した価格と直接の相関関係がある.3つの企業間の価格戦争について考える.各企業にそれぞれ低価格と高価格の選択肢がある:
関連するガイド
-
▪
- ゲーム理論
テキスト
Wolfram Research (2025), MatrixGamePlot, Wolfram言語関数, https://reference.wolfram.com/language/ref/MatrixGamePlot.html.
CMS
Wolfram Language. 2025. "MatrixGamePlot." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MatrixGamePlot.html.
APA
Wolfram Language. (2025). MatrixGamePlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixGamePlot.html
BibTeX
@misc{reference.wolfram_2025_matrixgameplot, author="Wolfram Research", title="{MatrixGamePlot}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/MatrixGamePlot.html}", note=[Accessed: 14-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_matrixgameplot, organization={Wolfram Research}, title={MatrixGamePlot}, year={2025}, url={https://reference.wolfram.com/language/ref/MatrixGamePlot.html}, note=[Accessed: 14-February-2026]}