MatrixGamePlot[mgame]
生成 MatrixGame mgame 的图表.
MatrixGamePlot[mgame,strat]
突出显示博弈策略 strat.


MatrixGamePlot
MatrixGamePlot[mgame]
生成 MatrixGame mgame 的图表.
MatrixGamePlot[mgame,strat]
突出显示博弈策略 strat.
更多信息和选项




- MatrixGamePlot 通常用于交流和理解矩阵博弈.
- 在双人博弈中,有一个收益向量矩阵. 每个向量代表每个玩家的收益.
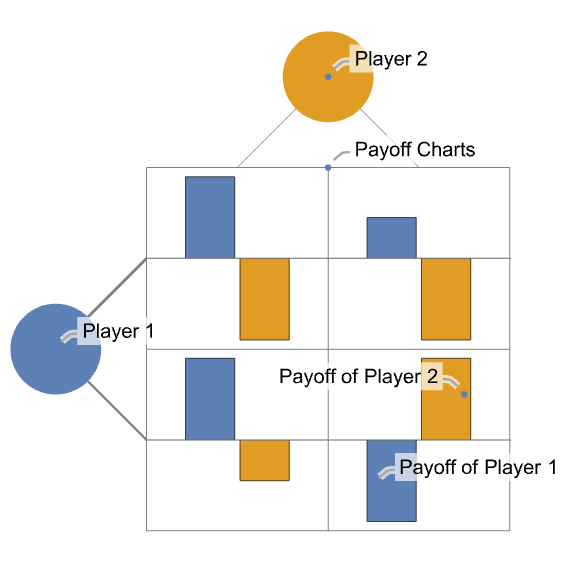
- 以下是双人博弈的图表,其中收益以图表形式绘制,并根据玩家标注不同颜色:
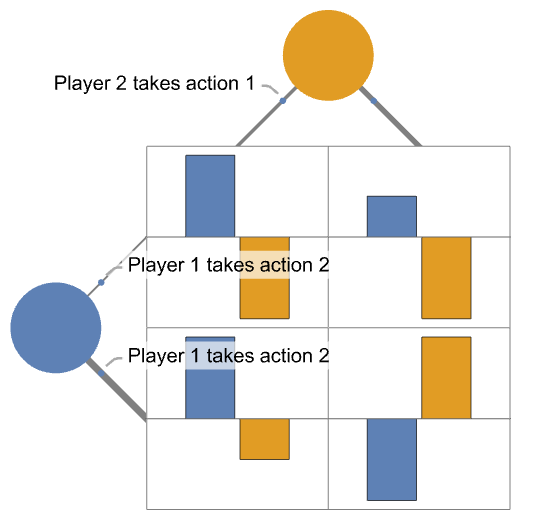
- 策略也可以通过玩家行或列上线条的粗细来表示. 玩家动作的顺序是从上到下、从左到右:
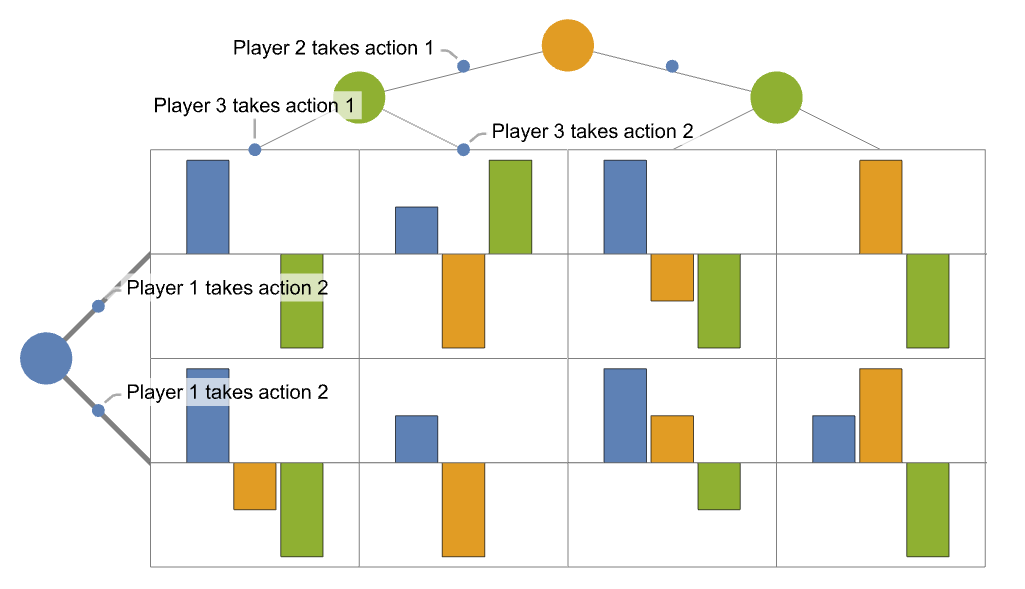
- 当行或列上有多个玩家时,行或列用于玩家动作的每个组合:
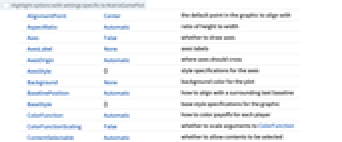
- MatrixGamePlot 具有与 Graphics 相同的选项,但有以下添加和更改: [所有选项的列表]
-
ColorFunction Automatic 如何为每个玩家的收益着色 ColorFunctionScaling False 是否缩放 ColorFunction 的参数 GameActionLabels Automatic 用于动作的标签 GamePlayerLabels Automatic 用于玩家的标签 PlotLayout Automatic 指定方块和行的布局 PlotLegends Automatic 收益值的图例 - ColorData["DefaultPlotColors"] 给出 ColorFunction 使用的默认颜色序列.
- PlotLayout 的可能设置包括:
-
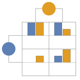
"BarChart" 将各收益方格绘制为 BarChart 
"SplitSquare" 将各收益方格绘制为分割方格 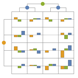
{{r1,…,rk},{c1,…,cn-k}} 更改行玩家和列玩家 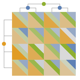
{"SplitSquare",{{…},{…}}} 合并前两个选项 - 请注意,收益数组可以重组为一个矩阵,其中玩家 {r1,…,rk} 为行玩家, {c1,…,cn-k} 为列玩家. 例如,如果有 5 个玩家,则默认顺序可能会将前两名玩家 ({1,2}) 划分为行,将其他三个玩家 ({3,4,5}) 划分为列. 使用此选项可以更改此顺序.
所有选项的列表


范例
打开所有单元 关闭所有单元基本范例 (4)
使用与 GameActionLabels 数组相同维度的数组显示策略:
范围 (5)
选项 (6)
ColorFunction (1)
指定 ColorData 中所示的配色方案:
PlotLayout (1)
应用 (9)
休闲游戏 (2)
社会学博弈 (1)
囚徒困境 (2)
经济学博弈 (3)
三个饿汉去餐馆吃饭,决定在点餐之前平摊账单. 餐厅有便宜、普通和昂贵三种餐点可供选择. 将这种情况表示为 MatrixGame:
古诺寡头垄断博弈(Cournot Oligopoly game)描述了这样一种情况,一组企业生产相同商品,其中每家企业都必须考虑生产成本和其他企业的产量. 只有价格最低的企业才能卖出商品.
这是符合直觉的,因为考虑到对于所有玩家来说,第二个动作的收益最大:
价格战是指这样一种博弈:多个企业都有兴趣提供最低价格,但每个企业的收益都与其选择的价格直接相关. 考虑三家企业之间的价格战,其中每家企业都可以在低价和高价之间做出选择:
相关指南
-
▪
- 博弈论
文本
Wolfram Research (2025),MatrixGamePlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MatrixGamePlot.html.
CMS
Wolfram 语言. 2025. "MatrixGamePlot." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MatrixGamePlot.html.
APA
Wolfram 语言. (2025). MatrixGamePlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MatrixGamePlot.html 年
BibTeX
@misc{reference.wolfram_2025_matrixgameplot, author="Wolfram Research", title="{MatrixGamePlot}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/MatrixGamePlot.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_matrixgameplot, organization={Wolfram Research}, title={MatrixGamePlot}, year={2025}, url={https://reference.wolfram.com/language/ref/MatrixGamePlot.html}, note=[Accessed: 06-February-2026]}