MaxValue

MaxValue[f,x]

gives the maximum value of f with respect to x.

MaxValue[f,{x,y,…}]

gives the maximum value of f with respect to x, y, ….

MaxValue[{f,cons},{x,y,…}]

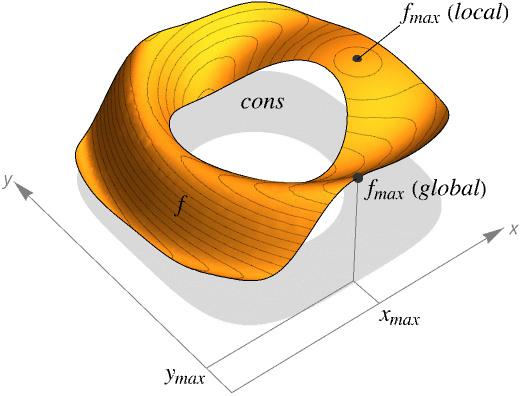
gives the maximum value of f subject to the constraints cons.

MaxValue[…,x∈rdom]

constrains x to be in the region or domain rdom.

MaxValue[…,…,dom]

constrains variables to the domain dom, typically Reals or Integers.

Details and Options

  • MaxValue is also known as supremum.
  • MaxValue finds the global maximum of f subject to the constraints given.
  • MaxValue is typically used to find the largest possible values given constraints. In different areas, this may be called the best strategy, best fit, best configuration and so on.
  • Maximize returns a list of the form {fmax,{x->xmax,y->ymax,…}}.
  • If f and cons are linear or polynomial, MaxValue will always find the global supremum.
  • The constraints cons can be any logical combination of:
  • lhs==rhsequations
    lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhsinequalities (LessEqual,…)
    lhsrhs, lhsrhs, lhsrhs, lhsrhsvector inequalities (VectorLessEqual,…)
    Exists[…], ForAll[…]quantified conditions
    {x,y,…}∈rdomregion or domain specification
  • MaxValue[{f,cons},x∈rdom] is effectively equivalent to MaxValue[{f,cons∧x∈rdom},x].
  • For x∈rdom, the different coordinates can be referred to using Indexed[x,i].
  • Possible domains rdom include:
  • Realsreal scalar variable
    Integersinteger scalar variable
    Vectors[n,dom]vector variable in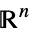
    Matrices[{m,n},dom]matrix variable in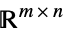
    ℛvector variable restricted to the geometric region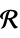
  • By default, all variables are assumed to be real.
  • MaxValue will return exact results if given exact input. With approximate input, it automatically calls NMaxValue.
  • MaxValue will return the following forms:
  • fmaxfinite maximum
    -∞infeasible, i.e. the constraint set is empty
    ∞unbounded, i.e. the values of f can be arbitrarily large
  • MaxValue gives the supremum of values of f. It may not be attained for any values of x, y, ….
  • N[MaxValue[…]] calls NMaxValue for optimization problems that cannot be solved symbolically.

Examples

open allclose all

Basic Examples  (5)

Find the maximum value of a univariate function:

Find the maximum value of a multivariate function:

Find the maximum value of a function subject to constraints:

Find the maximum value as a function of parameters:

Find the maximum value of a function over a geometric region:

Scope  (36)

Basic Uses  (7)

Maximize over the unconstrained reals:

Maximize subject to constraints :

Constraints may involve arbitrary logical combinations:

An unbounded problem:

An infeasible problem:

The supremum value may not be attained:

Use a vector variable and a vector inequality:

Univariate Problems  (7)

Unconstrained univariate polynomial maximization:

Constrained univariate polynomial maximization:

Exp-log functions:

Analytic functions over bounded constraints:

Periodic functions:

Combination of trigonometric functions with commensurable periods:

Combination of periodic functions with incommensurable periods:

Piecewise functions:

Unconstrained problems solvable using function property information:

Multivariate Problems  (9)

Multivariate linear constrained maximization:

Linear-fractional constrained maximization:

Unconstrained polynomial maximization:

Constrained polynomial optimization can always be solved:

The maximum value may not be attained:

The objective function may be unbounded:

There may be no points satisfying the constraints:

Quantified polynomial constraints:

Algebraic maximization:

Bounded transcendental maximization:

Piecewise maximization:

Convex maximization:

Maximize concave objective function such that is positive semidefinite and :

Plot the function and the maximum value over the region:

Parametric Problems  (4)

Parametric linear optimization:

The maximum value is a continuous function of parameters:

Parametric quadratic optimization:

The maximum value is a continuous function of parameters:

Unconstrained parametric polynomial maximization:

Constrained parametric polynomial maximization:

Optimization over Integers  (3)

Univariate problems:

Integer linear programming:

Polynomial maximization over the integers:

Optimization over Regions  (6)

Find the maximum value of a function over a geometric region:

Plot it:

Find the maximum distance between points in two regions:

Find the maximum such that the triangle and ellipse still intersect:

Plot it:

Find the maximum for which contains the given three points:

Use to specify that is a vector in :

Find the maximum distance between points in two regions:

Options  (1)

WorkingPrecision  (1)

Finding the exact maximum can take a long time:

With WorkingPrecision->200, you get an exact maximum value, but it might be incorrect:

Applications  (13)

Basic Applications  (4)

Find the maximal area among rectangles with a unit perimeter:

Find the maximal area among triangles with a unit perimeter:

Find the maximum height reached by a projectile:

Find the maximum range of a projectile:

The infinity norm of a function f[x] is given by MaxValue[{Norm[f[x]],x∈},x] where is the domain of interest for f[x]. Find the infinity norm of over the interval {-3,3}:

Plot it:

Find the infinity norm for over Rectangle[{-1,-1},{1,1}]:

Plot it:

Geometric Distances  (9)

The largest distance of a point in a region ℛ to a given point p is given by MaxValue[EuclideanDistance[p,q],q∈ℛ]. Find the largest distance of a point in the unit Disk[] to the point {1,1} :

Plot it:

Find the largest distance of a point in the standard unit simplex Simplex[2] to the point {1,3/4}:

Plot it:

Find the largest distance of a point in the standard unit sphere Sphere[] to the point {1,1,1}:

Plot it:

Find the largest distance of a point in the standard unit simplex Simplex[3] to the point {-1/3,1/3,1/3}:

Plot it:

The diameter of a region ℛ is the maximum distance between two points in ℛ. It can be computed through MaxValue[EuclideanDistance[p,q],{p∈ℛ,q∈ℛ}]. Find the diameter of Circle[]:

Find the diameter of the standard unit simplex Simplex[2]:

Find the diameter of the standard unit cube Cuboid[]:

The largest distance of points p∈ and q∈ can be found through MaxValue[EuclideanDistance[p,q],{p∈,q∈}]. Find the largest distance of points in Disk[{0,0}] and Rectangle[{3,3}]:

Find the largest distance of points in Line[{{0,0,0},{1,1,1}}] and Ball[{5,5,0},1]:

Properties & Relations  (4)

Maximize gives both the value of the maximum and the maximizer point:

MaxValue gives an exact global maximum value of the objective function:

NMaxValue attempts to find a global maximum numerically, but may find a local maximum:

FindMaxValue finds local maxima depending on the starting point:

MaxValue can solve linear programming problems:

LinearProgramming can be used to solve the same problem given in matrix notation:

Use RegionBounds to compute the bounding box:

Use MaxValue and MinValue to compute the same bounds:

Possible Issues  (1)

MaxValue requires that all functions present in the input be real-valued:

Values for which the equation is satisfied but the square roots are not real are disallowed:

Wolfram Research (2008), MaxValue, Wolfram Language function, https://reference.wolfram.com/language/ref/MaxValue.html (updated 2021).

Text

Wolfram Research (2008), MaxValue, Wolfram Language function, https://reference.wolfram.com/language/ref/MaxValue.html (updated 2021).

CMS

Wolfram Language. 2008. "MaxValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/MaxValue.html.

APA

Wolfram Language. (2008). MaxValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MaxValue.html

BibTeX

@misc{reference.wolfram_2024_maxvalue, author="Wolfram Research", title="{MaxValue}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/MaxValue.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_maxvalue, organization={Wolfram Research}, title={MaxValue}, year={2021}, url={https://reference.wolfram.com/language/ref/MaxValue.html}, note=[Accessed: 14-November-2024 ]}