MinimalPolynomial[s,x]
gives the minimal polynomial in x for which the algebraic number s is a root.
MinimalPolynomial[u,x]
gives the minimal polynomial of the finite field element u over ![]() .
.
MinimalPolynomial[u,x,k]
gives the minimal polynomial of u over the ![]() -element subfield of the ambient field of u.
-element subfield of the ambient field of u.
MinimalPolynomial[u,x,emb]
gives the minimal polynomial of u relative to the finite field embedding emb.


MinimalPolynomial
MinimalPolynomial[s,x]
gives the minimal polynomial in x for which the algebraic number s is a root.
MinimalPolynomial[u,x]
gives the minimal polynomial of the finite field element u over ![]() .
.
MinimalPolynomial[u,x,k]
gives the minimal polynomial of u over the ![]() -element subfield of the ambient field of u.
-element subfield of the ambient field of u.
MinimalPolynomial[u,x,emb]
gives the minimal polynomial of u relative to the finite field embedding emb.
Details and Options

- MinimalPolynomial[s,x] gives the lowest-degree polynomial with integer coefficients, positive leading coefficient and the GCD of all coefficients equal to
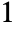 for which the algebraic number s is a root.
for which the algebraic number s is a root. - MinimalPolynomial[s] gives a pure function representation of the minimal polynomial of s.
- MinimalPolynomial[s,x,Extension->a] finds the characteristic polynomial of
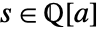 over the field
over the field 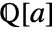 .
. - For a FiniteFieldElement object u in a finite field
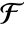 of characteristic
of characteristic 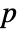 , MinimalPolynomial[u, x] gives the lowest-degree monic polynomial with integer coefficients between
, MinimalPolynomial[u, x] gives the lowest-degree monic polynomial with integer coefficients between 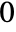 and
and 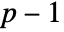 for which u is a root.
for which u is a root. - MinimalPolynomial[u,x,k] gives the lowest-degree monic polynomial with coefficients from the
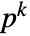 -element subfield of
-element subfield of 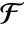 for which u is a root. k needs to be a divisor of the extension degree of
for which u is a root. k needs to be a divisor of the extension degree of 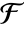 over
over 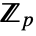 .
. - If emb=FiniteFieldEmbedding[e1e2], then MinimalPolynomial[u,x,emb] gives the polynomial with coefficients in the ambient field of e1 that map through emb to the coefficients of the minimal polynomial of u over the image of emb.
Examples
open all close allBasic Examples (2)
Scope (6)
Algebraic Numbers (5)
Finite Field Elements (1)
Options (1)
Applications (3)
Properties & Relations (6)
Compute the extension that defines the number field ![]() :
:
Find the characteristic polynomial of ![]() over
over ![]() :
:
The characteristic polynomial is a power of the minimal polynomial of ![]() :
:
Use FrobeniusAutomorphism to find all conjugates of a finite field element a:
The conjugates are roots of the minimal polynomial of a:
If MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0, then ![]() :
:
If MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0, then ![]() :
:
If MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0, then ![]() :
:
If MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0, then ![]() :
:
Tech Notes
Related Guides
Text
Wolfram Research (2007), MinimalPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/MinimalPolynomial.html (updated 2023).
CMS
Wolfram Language. 2007. "MinimalPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/MinimalPolynomial.html.
APA
Wolfram Language. (2007). MinimalPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MinimalPolynomial.html
BibTeX
@misc{reference.wolfram_2025_minimalpolynomial, author="Wolfram Research", title="{MinimalPolynomial}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/MinimalPolynomial.html}", note=[Accessed: 14-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_minimalpolynomial, organization={Wolfram Research}, title={MinimalPolynomial}, year={2023}, url={https://reference.wolfram.com/language/ref/MinimalPolynomial.html}, note=[Accessed: 14-January-2026]}