MinimalPolynomial
MinimalPolynomial[s,x]
代数的数 s が根である,x の最小多項式を返す.
MinimalPolynomial[u,x]
![]() 上で有限体の元 u の最小多項式を与える.
上で有限体の元 u の最小多項式を与える.
MinimalPolynomial[u,x,k]
u の周辺体の ![]() 元の部分体上で u の最小多項式を与える.
元の部分体上で u の最小多項式を与える.
MinimalPolynomial[u,x,emb]
有限体の埋込み emb と相対的な u の最小多項式を与える.
詳細とオプション

- MinimalPolynomial[s,x]は,整数係数,正の首位次数の係数,代数的数 s が根である
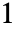 と等しいすべての係数のGCDを持つ最低次数の多項式を与える.
と等しいすべての係数のGCDを持つ最低次数の多項式を与える. - MinimalPolynomial[s]は,s の最小多項式を純関数で表したものを返す.
- MinimalPolynomial[s,x,Extension->a]は,体
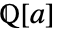 上で
上で 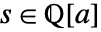 の特性多項式を求める.
の特性多項式を求める. - 標数
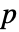 の有限体
の有限体 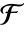 内のFiniteFieldElementオブジェクト u について,MinimalPolynomial[u, x]は,u が根である,
内のFiniteFieldElementオブジェクト u について,MinimalPolynomial[u, x]は,u が根である,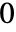 から
から 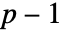 までの整数係数を持つ最低次数のモニック多項式を与える.
までの整数係数を持つ最低次数のモニック多項式を与える. - MinimalPolynomial[u,x,k]は u が根である
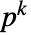 元の部分体
元の部分体 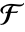 からの係数を持つ最低次数のモニック多項式を与える.k は
からの係数を持つ最低次数のモニック多項式を与える.k は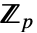 上の
上の 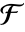 の拡大次数の除数でなければならない.
の拡大次数の除数でなければならない. - emb=FiniteFieldEmbedding[e1e2]なら,MinimalPolynomial[u,x,emb]は emb を介して emb の像の上で u の最小多項式の係数へ写像する e1の周辺体の係数を持つ多項式を与える.
例題
すべて開くすべて閉じるスコープ (6)
代数的数 (5)
特性と関係 (6)
FrobeniusAutomorphismを使って有限体の元 a のすべての共役を求める:
MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0なら![]() である:
である:
MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0なら![]() である:
である:
MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0なら ![]() である:
である:
MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0なら ![]() である:
である:
テキスト
Wolfram Research (2007), MinimalPolynomial, Wolfram言語関数, https://reference.wolfram.com/language/ref/MinimalPolynomial.html (2023年に更新).
CMS
Wolfram Language. 2007. "MinimalPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/MinimalPolynomial.html.
APA
Wolfram Language. (2007). MinimalPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MinimalPolynomial.html