MinimalPolynomial
MinimalPolynomial[s,x]
给出关于 x 的最小多项式,代数数 s 是它的一个根.
MinimalPolynomial[u,x]
给出有限域元素 u 在 ![]() 上的最小多项式.
上的最小多项式.
MinimalPolynomial[u,x,k]
给出 u 在环绕域 (ambient field) 的 ![]() -元素子域上 u 的最小多项式.
-元素子域上 u 的最小多项式.
MinimalPolynomial[u,x,emb]
给出 u 相对于有限域嵌入 emb 的最小多项式.
更多信息和选项

- MinimalPolynomial[s,x] 给出具有整数系数、正首项系数、所有系数的 GCD 等于
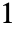 且代数数 s 是一个根的最低次多项式.
且代数数 s 是一个根的最低次多项式. - MinimalPolynomial[s] 给出 s 的最小多项式的纯函数表示.
- MinimalPolynomial[s,x,Extension->a] 在域
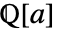 上求
上求 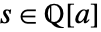 的特征多项式.
的特征多项式. - 对于特征为
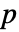 的有限域
的有限域 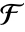 中的 FiniteFieldElement 对象 u,MinimalPolynomial[u, x] 给出整数系数在
中的 FiniteFieldElement 对象 u,MinimalPolynomial[u, x] 给出整数系数在 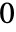 到
到 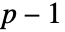 之间且 u 为根的次数最低的一元多项式.
之间且 u 为根的次数最低的一元多项式. - MinimalPolynomial[u,x,k] 给出次数最低的一元多项式,其系数来自
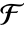 的
的 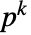 -元素子域,其中 u 是一个根. k 应为
-元素子域,其中 u 是一个根. k 应为 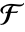 的扩张次数 (extension degree) 在
的扩张次数 (extension degree) 在 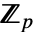 上的除数.
上的除数. - 如果 emb=FiniteFieldEmbedding[e1e2],则 MinimalPolynomial[u,x,emb] 给出系数位于 e1 的环绕域中的多项式,通过 emb 映射到 u 在 emb 图像上的最小多项式的系数.
范例
打开所有单元关闭所有单元范围 (6)
代数数 (5)
属性和关系 (6)
用 FrobeniusAutomorphism 求有限域元素 a 的所有共轭:
如果 MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0,则 ![]() :
:
如果 MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0,则 ![]() :
:
如果 MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0,则 ![]() :
:
如果 MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0,则 ![]() :
:
文本
Wolfram Research (2007),MinimalPolynomial,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MinimalPolynomial.html (更新于 2023 年).
CMS
Wolfram 语言. 2007. "MinimalPolynomial." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/MinimalPolynomial.html.
APA
Wolfram 语言. (2007). MinimalPolynomial. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MinimalPolynomial.html 年