NCaputoD
NCaputoD[f,{x,α},x0]
関数 f の点 x0における α 階Caputo非整数階微分![]() の数値近似を与える.
の数値近似を与える.
詳細とオプション

- NCaputoDは f のCaputo微積分としても知られているCaputoDの数値バージョンである.
-
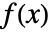 の
の 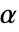 階Caputo非整数階微分は
階Caputo非整数階微分は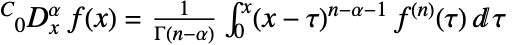 と定義される.ただし,
と定義される.ただし,![n=max(0,TemplateBox[{alpha}, Ceiling]) n=max(0,TemplateBox[{alpha}, Ceiling])](Files/NCaputoD.ja/5.png) である.
である. - NCaputoDは,一般に,CaputoDによる記号計算が失敗した場合に使われる.
- 次は,NCaputoDに与えられるオプションである.
-
AccuracyGoal Infinity 目標確度の桁数 PrecisionGoal Automatic 目標精度の桁数 WorkingPrecision MachinePrecision 内部計算精度
例題
すべて開くすべて閉じる例 (4)
二次関数の1/2階Caputo微分を任意の点で x について計算する:
MittagLefflerEの数値Caputo非整数階微分を任意の点で計算する:
MittagLefflerE関数のCaputo非整数階微分の数値リストを生成する:
スコープ (8)
アプリケーション (3)
特性と関係 (4)
NCaputoDはすべての実数 ![]() について定義される:
について定義される:
数値NCaputoDのアプローチでCaputo非整数階微分をプロットする:
記号CaputoDのアプローチと比較する:
NCaputoDは負の階数 ![]() についてはNFractionalDに等しい:
についてはNFractionalDに等しい:
考えられる問題 (2)
おもしろい例題 (1)
Sin関数とその半階,1階,![]() 階微分をプロットする:
階微分をプロットする:
テキスト
Wolfram Research (2022), NCaputoD, Wolfram言語関数, https://reference.wolfram.com/language/ref/NCaputoD.html.
CMS
Wolfram Language. 2022. "NCaputoD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NCaputoD.html.
APA
Wolfram Language. (2022). NCaputoD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NCaputoD.html