Nearest

Nearest[{elem1,elem2,…},x]

gives the list of elemi to which x is nearest.

Nearest[{elem1v1,elem2v2,…},x]

gives the vi corresponding to the elemi to which x is nearest.

Nearest[{elem1,elem2,…}{v1,v2,…},x]

gives the same result.

Nearest[{elem1,elem2,…}prop,x]

gives the property prop for the elemi to which x is nearest.

Nearest[data,{x1,x2,…}]

effectively gives {Nearest[data,x1],Nearest[data,x2],…}.

Nearest[data,x,n]

gives the n nearest elemi to x.

Nearest[data,x,{n,r}]

gives the n or fewer nearest elemi to x that are within radius r of x.

Nearest[data]

generates a NearestFunction[…] that can be applied repeatedly to different x.

Details and Options

  • Nearest works for a variety of data, including numerical, geospatial, textual, and visual, as well as dates and times.
  • The data can also be given as an association. In this case, Nearest[<|key1val1,key2val2,…|>] is equivalent to Nearest[{val1key1,val2key2,…}].
  • In Nearest[{elem1,elem2,…}prop,…], possible forms for prop include:
  • "Element"the elemi found to be nearest
    "Index"the index i of the elemi found to be nearest
    "Distance"the distance to the nearest elemi
    {prop1,prop2,…}a list of multiple forms
    Allan association giving element, index and distance
  • When Nearest returns several elements elemi, the nearest ones are given first.
  • If several elements are at the same distance, they are returned in the order they appear in data.
  • Nearest[data,x,{All,r}] can be used to get all elemi within radius r.
  • The following options can be given:
  • DistanceFunction Automaticthe distance metric to use
    Method Automaticmethod to use
    WorkingPrecision Automaticprecision to use for numeric data
  • By default, the following distance functions are used for different types of elemi:
  • Norm[#1-#2]&numeric data
    JaccardDissimilarityBoolean data
    EditDistancestrings
    ColorDistancecolors
    ImageDistanceimages
    DateDifferencedates and times
    GeoDistancegeospatial data
  • Nearest with geospatial data uses GeoDistance to compute distances. The data can be given as a list of GeoPosition objects, or a GeoPosition containing an array of points.
  • For images or colors and a distance function f, DistanceFunction->f is passed to ImageDistance and ColorDistance, respectively. »
  • All images are conformed using ConformImages. With DistanceFunction->Automatic, dimensionality reduction based on discrete cosine transform is applied to the set of images.
  • Using Norm[#1-#2,p]& for 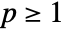or named distance functions such as ManhattanDistance, ChessboardDistance, and EuclideanDistance can invoke special optimizations for numeric vector data.
  • Possible settings for Method include "Octree", "KDtree", and "Scan".
  • Possible settings for the WorkingPrecision option are:
  • MachinePrecisionuse machine-precision numbers
    puse precision p
    Automaticuse adaptive precision to resolve nearest points

Examples

open allclose all

Basic Examples  (5)

Find the element nearest to 20:

Find the 3 elements nearest to 20:

Find which element is nearest to {2,3} in 2D:

Find "nearest" strings:

Find nearest colors:

Find the nearest image partition to a subimage:

Scope  (9)

Give the 3 nearest elements:

Give the elements within radius 2:

Give at most 3 nearest elements within radius 2:

Find the nearest matrix:

Find which element is nearest to {2,3} in 2D and return the appropriate label:

Compute the same using an Association:

Return the index for the nearest string:

Return an Association giving the string element, index, and distance:

Find the 3 elements nearest to 20, simultaneously reporting the elements and their distance to 20:

For uniform random points in 3D, give the distances for the 10 nearest to the origin:

For each of the 10 nearest, give an Association including the point element, index and distance:

Create a lookup function for future use:

Find the date nearest to a given DateObject:

Find out which of these {lat,lon} points on Earth is closest to you:

Express the input as a list of separate GeoPosition objects instead:

Report simultaneously the closest point and the distance to it:

Options  (6)

DistanceFunction  (3)

By default, normal Euclidean distance is used for points:

Use the ManhattanDistance, which sums the length of each side:

The ChessboardDistance only takes into account the dimension with the largest separation:

The DistanceFunction can be given as a symbol:

Or as a pure function:

Find nearest colors using a color distance different from the default distance in ColorDistance:

Method  (2)

Compare different methods for machine-precision data:

In three dimensions, the "KDtree" method is faster:

In 20 dimensions, a simple scan is faster:

The setting Method->{"KDtree","LeafSize"->s} may be used to control the maximum number of points in any leaf of the KD tree constructed:

Plot the tree setup time:

Plot the lookup time for different points:

WorkingPrecision  (1)

Using WorkingPrecision->MachinePrecision ensures the fastest evaluation method is used:

The results may not be correct if the numbers are not all distinct to machine precision:

All the points are effectively the same to machine precision:

An appropriate higher value of precision will work:

Applications  (8)

Plot the Nearest of a list of:

Create a Voronoi diagram:

Use higher resolution:

Use a 1-norm ("taxicab distance"):

Highlight the 200 random points closest to the origin:

Use the "taxicab" metric:

Create a nearest function from all the words in a dictionary:

Look up words closest to a given word:

Go farther:

Find the outputs from running a sequence of elementary cellular automata:

Generate a complete list of outputs from all 256 elementary cellular automata:

Find which rules give outputs nearest the specified sequences:

Use a negative distance function to find the element farthest away from the given element:

Show the returned element for all values between 1 and 5:

Take the polygon of Mexico:

Compute the nearest of the points of that polygon from your current geo location:

Draw the geodesic from your location to that point:

Properties & Relations  (2)

In the case of a tie, all nearest elements are returned in order:

The single argument form of Nearest returns a NearestFunction object:

This is an optimized lookup function, which is faster than calling Nearest repeatedly:

Neat Examples  (1)

Find successive nearest words in a dictionary:

Wolfram Research (2007), Nearest, Wolfram Language function, https://reference.wolfram.com/language/ref/Nearest.html (updated 2017).

Text

Wolfram Research (2007), Nearest, Wolfram Language function, https://reference.wolfram.com/language/ref/Nearest.html (updated 2017).

CMS

Wolfram Language. 2007. "Nearest." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/Nearest.html.

APA

Wolfram Language. (2007). Nearest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Nearest.html

BibTeX

@misc{reference.wolfram_2024_nearest, author="Wolfram Research", title="{Nearest}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/Nearest.html}", note=[Accessed: 18-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_nearest, organization={Wolfram Research}, title={Nearest}, year={2017}, url={https://reference.wolfram.com/language/ref/Nearest.html}, note=[Accessed: 18-December-2024 ]}