Nearest[{elem1,elem2,…},x]
x に最も近い elemiのリストを与える.
Nearest[{elem1v1,elem2v2,…},x]
x に最も近い elemiに対応する viを与える.
Nearest[{elem1,elem2,…}{v1,v2,…},x]
同じ結果を与える.
Nearest[{elem1,elem2,…}prop,x]
x が最も近い elemiの特性 prop を与える.
Nearest[data,{x1,x2,…}]
事実上,{Nearest[data,x1],Nearest[data,x2],…}を与える.
Nearest[data,x,n]
x に最も近い n 個の elemiを与える.
Nearest[data,x,{n,r}]
x の半径 r 内にある,x に最も近い n 個以下の elemiを与える.
Nearest[data]
異なる x に繰り返し適用可能なNearestFunction[…]を生成する.


Nearest
Nearest[{elem1,elem2,…},x]
x に最も近い elemiのリストを与える.
Nearest[{elem1v1,elem2v2,…},x]
x に最も近い elemiに対応する viを与える.
Nearest[{elem1,elem2,…}{v1,v2,…},x]
同じ結果を与える.
Nearest[{elem1,elem2,…}prop,x]
x が最も近い elemiの特性 prop を与える.
Nearest[data,{x1,x2,…}]
事実上,{Nearest[data,x1],Nearest[data,x2],…}を与える.
Nearest[data,x,n]
x に最も近い n 個の elemiを与える.
Nearest[data,x,{n,r}]
x の半径 r 内にある,x に最も近い n 個以下の elemiを与える.
Nearest[data]
異なる x に繰り返し適用可能なNearestFunction[…]を生成する.
詳細とオプション



- Nearestは,数値データ,地理空間データ,テキストデータ,視覚データを含むさまざまなデータおよび日付や時刻に使うことができる.
- データは連想として与えることもできる.この場合,Nearest[<|key1val1,key2val2,…|>]はNearest[{val1key1,val2key2,…}]に等しい.
- 以下は,Nearest[{elem1,elem2,…}prop,…]で prop の取り得る形である.
-
"Element" 最も近いことが分かった elemi "Index" 最も近いことが分かった elemiの指標 i "Distance" 最も近い elemiまでの距離 {prop1,prop2,…} 複数の形式のリスト All 要素,指標,距離を与える連想 - Nearestが複数の要素 elemiを返す場合が,最も近いものが先頭に置かれる.
- 複数の要素が等距離にある場合は,data 中の出現順で返される.
- Nearest[data,x,{All,r}]を使って半径 r 内のすべての elemiを得ることができる.
- 次のオプションが与えられる.
-
DistanceFunction Automatic 使用する距離尺度 Method Automatic 使用するメソッド WorkingPrecision Automatic 数値データに使用する精度 - デフォルトで,異なるタイプの elemiに次の距離関数を使うことができる.
-
Norm[#1-#2]& 数値データ JaccardDissimilarity ブールデータ EditDistance 文字列 ColorDistance 色 ImageDistance 画像 DateDifference 日付と時刻 GeoDistance 地理空間データ - 地理空間データを伴うNearestはGeoDistance使って距離を計算する.データはGeoPositionオブジェクトのリストとして,あるいは点の配列を含むGeoPositionとして与えることができる.
- 画像あるいは色および距離関数 f について,DistanceFunction->f はそれぞれImageDistanceおよびColorDistanceに渡される. »
- 画像はすべてはConformImagesを使って統一される.DistanceFunction->Automaticのとき,離散余弦変換に基づく次元縮退が画像の集合に適用される.
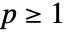 についてNorm[#1-#2,p]&またはManhattanDistance,ChessboardDistance,EuclideanDistance等の名前付きの距離関数を使うと,数値ベクトルデータに対しての特別の最適化が呼び出される.
についてNorm[#1-#2,p]&またはManhattanDistance,ChessboardDistance,EuclideanDistance等の名前付きの距離関数を使うと,数値ベクトルデータに対しての特別の最適化が呼び出される.- Methodに使用可能な設定値には"Octree","KDtree","Scan"がある.
- WorkingPrecisionオプションの使用可能な設定値
-
MachinePrecision 機械精度数を使う p 精度 p を使う Automatic 最近点を求めるために適応的精度を使う
例題
すべて開く すべて閉じる例 (5)
スコープ (9)
Associationを使って同じ計算をする:
文字列要素,指標,距離を与えるAssociationを返す:
20に最も近い要素を3つ求め,同時に要素と20までの距離をレポートする:
一様ランダム分布に従う3Dの点について,原点に最も近い10の点の距離を与える:
最も近い10の点のそれぞれについて,点要素,指標,距離を含むAssociationを与える:
与えられたDateObjectに最も近いデータを求める:
地球上の{lat,lon}点のいずれがユーザに最も近いかを求める:
入力を別々のGeoPositionオブジェクトのリストとして表す:
オプション (6)
DistanceFunction (3)
各側の長さを合計するManhattanDistanceを用いる:
ChessboardDistanceは最大距離間隔の次元のみを考慮する:
DistanceFunctionは記号として与えることができる:
ColorDistanceにおけるデフォルト距離とは異なる色距離を使って最も近い色を求める:
Method (2)
Method->{"KDtree","LeafSize"->s}の設定を使って,構築されたKDツリーの任意の葉の最大点数を制御することができる:
WorkingPrecision (1)
WorkingPrecision->MachinePrecisionを使うと,最も速い評価法が確実に使われる:
アプリケーション (8)
特性と関係 (2)
Nearestの1引数形式はNearestFunctionオブジェクトを返す:
これは,繰り返しNearestを呼ぶよりも速い,最適化された検索関数である:
テクニカルノート
-
▪
- データのクラスタ分割 ▪
- Nearestを使う
関連するガイド
-
▪
- 論理演算とブール代数 ▪
- ブール計算 ▪
- 計算幾何学 ▪
- 教師あり機械学習 ▪
- テキスト解析 ▪
- 自然言語処理 ▪
- 配列アラインメントと比較 ▪
- 距離と類似度の測定基準 ▪
- 日付と時刻 ▪
- 機械学習 ▪
- 科学的モデル ▪
- 言語学データ ▪
- リストへの数学的およびカウント操作 ▪
- コンピュータビジョン ▪
- 音声解析 ▪
- 音声処理 ▪
- 音声計算
テキスト
Wolfram Research (2007), Nearest, Wolfram言語関数, https://reference.wolfram.com/language/ref/Nearest.html (2017年に更新).
CMS
Wolfram Language. 2007. "Nearest." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/Nearest.html.
APA
Wolfram Language. (2007). Nearest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Nearest.html
BibTeX
@misc{reference.wolfram_2025_nearest, author="Wolfram Research", title="{Nearest}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/Nearest.html}", note=[Accessed: 02-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_nearest, organization={Wolfram Research}, title={Nearest}, year={2017}, url={https://reference.wolfram.com/language/ref/Nearest.html}, note=[Accessed: 02-February-2026]}