Orthogonalize
Orthogonalize[{v1,v2,…}]
ベクトル viを直交させることによって見付かる正規直交基底を返す.
Orthogonalize[{e1,e2,…},f]
内積関数 f と要素 eiを直交させることで求まる直交基底を返す.
詳細とオプション

- Orthogonalize[{v1,v2,…}]は,内積として通常のスカラー積
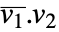 を用いる.
を用いる. - Orthogonalizeの出力は常に入力と同じ数のベクトルを含んでいる.入力ベクトルの中に線形非従属ではないものがある場合,出力にはゼロベクトルが含まれる.
- 出力中の非ゼロベクトルはすべて単位長に正規化される.
- 内積関数 f は,eiの線形結合のペアに適用される.
- eiは f が常に実数の結果を与える任意の式でよい. »
- Orthogonalize[{v1,v2,…},Dot]は,実質的に viの要素はすべて実数であるとみなす. »
- Orthogonalizeはデフォルトでグラム・シュミット(Gram–Schmidt)基底を生成する.
- Methodオプションの設定値を変えることで,他の基底を得ることができる.可能な設定値には"GramSchmidt","ModifiedGramSchmidt","Reorthogonalization","Householder"等がある.
- Orthogonalize[list,Tolerance->t]は相対的なノルムが t よりも下になるゼロ要素に設定する.
例題
すべて開くすべて閉じるスコープ (13)
基本的な用法 (6)
特殊行列 (4)
オプション (3)
アプリケーション (12)
幾何学 (3)
ベクトル ![]() をベクトル
をベクトル![]() とベクトル
とベクトル![]() でスパンされた平面上に射影する:
でスパンされた平面上に射影する:
フレネ・セレ(Frenet–Serret)の系はすべての空間曲線の特性をベクトル基底とスカラー関数で符号化する.次の曲線について考える:
Orthogonalizeを使って最初の3つの導関数から正規直交基底を構築する:
FrenetSerretSystemを使って答を確かめる:
最小二乗と曲線のフィット (3)
線形系 ![]() に解がない場合,最良の近似解は最小二乗解である.それは
に解がない場合,最良の近似解は最小二乗解である.それは ![]() の解である.ただし,
の解である.ただし,![]() は
は ![]() の列空間への
の列空間への ![]() の正射影である.次の
の正射影である.次の ![]() と
と ![]() について考える:
について考える:
LeastSquaresを使って結果を確認する:
Orthogonalizeを使ってデータに最もフィットする曲線が求められる.次のデータについて考える:
![]() を最小にすることが直線
を最小にすることが直線 ![]() にフィットさせることになるように,
にフィットさせることになるように,![]() に列
に列 ![]() と
と ![]() があるとする:
があるとする:
Fitを使って係数を確認する:
![]() を最小化することが
を最小化することが ![]() にフィットさせることになるように,
にフィットさせることになるように,![]() に列
に列 ![]() ,
,![]() ,
,![]() があるとする:
があるとする:
Fitを使って係数を確認する:
行列分解 (2)
次の行列 ![]() の列空間の正規直交基底を求め.その基底を使って
の列空間の正規直交基底を求め.その基底を使って ![]() のQR分解を求める:
のQR分解を求める:
グラム・シュミットを ![]() の列に適用し,次に列がそれらのベクトルである行列として
の列に適用し,次に列がそれらのベクトルである行列として ![]() を定義する:
を定義する:
QRDecompositionが与える結果と比較する. ![]() 行列は同じである:
行列は同じである:
QRDecompositionは行正規直交の結果を与えるので,![]() 行列は転置の分だけ違っている:
行列は転置の分だけ違っている:
エルミート行列(より一般的には,任意の正規行列)の固有ベクトルは直交ベクトルであり,射影行列は ![]() と定義するのが慣習的である.ただし,
と定義するのが慣習的である.ただし,![]() は正規化された固有ベクトルである.一般的なベクトルへの射影行列の作用が次の行列
は正規化された固有ベクトルである.一般的なベクトルへの射影行列の作用が次の行列 ![]() の固有空間にベクトルを射影することと同じであることを示す:
の固有空間にベクトルを射影することと同じであることを示す:
![]() と
と ![]() は異なる固有空間から来ているので,どちらも
は異なる固有空間から来ているので,どちらも ![]() に直交する:
に直交する:
両者は同じ固有値を持つので,互いに直交である必要はなく,直交してもいない:
Orthogonalizeを使って ![]() から正規直交基底を作成する:
から正規直交基底を作成する:
一般的なベクトルに ![]() を掛けると
を掛けると ![]() へのベクトルの射影と等しくなることを確認する:
へのベクトルの射影と等しくなることを確認する:
一般的な内積と関数空間 (4)
正定値であることは関連付けられた二次形式 ![]() が
が ![]() について正であることを意味する:
について正であることを意味する:
Dot自体が恒等行列に関連付けられた内積である点に注意のこと:
フーリエ級数は内積空間 ![]() における正規直交基底への射影である.自乗可積分関数上の標準的な内積を定義する:
における正規直交基底への射影である.自乗可積分関数上の標準的な内積を定義する:
![]() はFourierParameters{0,1}に対応する対称フーリエ係数に等しい:
はFourierParameters{0,1}に対応する対称フーリエ係数に等しい:
FourierCoefficientを使って確認する:
FourierSeriesを使って結果を確認する:
LegendrePは直交多項式族を内積![]() について定義する.
について定義する.![]() が0から4までのときに多項式
が0から4までのときに多項式 ![]() を直交化して最初のルジャンドル多項式のスカラー倍数を計算する:
を直交化して最初のルジャンドル多項式のスカラー倍数を計算する:
HermiteHは直交多項式族を内積![]() について定義する.正規化されていないグラム・シュミット過程を多項式
について定義する.正規化されていないグラム・シュミット過程を多項式 ![]() (
(![]() は0から4まで)に適用して最初の5つのエルミート多項式のスカラー倍数を計算する:
は0から4まで)に適用して最初の5つのエルミート多項式のスカラー倍数を計算する:
特性と関係 (9)
入力ベクトルが線形独立ではないなら,結果は零ベクトルで長さが揃うように充填される:
![]() がOrthogonalize[vecs]の結果なら,
がOrthogonalize[vecs]の結果なら,![]() は対角行列である:
は対角行列である:
ランダムな ![]() 次元のベクトル集合のほとんどは,厳密に
次元のベクトル集合のほとんどは,厳密に ![]() 基底ベクトルだけスパンされる:
基底ベクトルだけスパンされる:
デフォルトのメソッドでは,基底の最初の要素は常に最初のベクトルの倍数である:
OrthogonalizeはProjectionとNormalizeを繰り返し適用することで実装できる:
Orthogonalize[m]はQRDecomposition[Transpose[m]]に関連する:
テキスト
Wolfram Research (2007), Orthogonalize, Wolfram言語関数, https://reference.wolfram.com/language/ref/Orthogonalize.html.
CMS
Wolfram Language. 2007. "Orthogonalize." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Orthogonalize.html.
APA
Wolfram Language. (2007). Orthogonalize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Orthogonalize.html