PageRankCentrality

PageRankCentrality[g,α]

グラフ g の頂点の重み α のページランク中心性のリストを与える．

PageRankCentrality[g,α,β]

重み α と初期中心性 β を使ったページランク中心性のリストを与える．

PageRankCentrality[{vw,…},…]

規則 vw を使って群 g を指定する．

詳細とオプション

  • ページランク中心性は，ランダムにリンクを辿っている人がWebグラフ上の任意の特定のページに辿り着く尤度を表す．
  • PageRankCentralityは c=alpha TemplateBox[{a}, Transpose].d.c+beta の解である中心性のリストを与える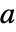． は g の隣接行列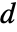， は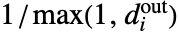からなる対角行列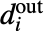（ は 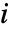番目の頂点の出次数）である． »
  • β がスカラーのとき，それは{β,β,…}を意味するものと解釈される．
  • PageRankCentrality[g,α]はPageRankCentrality[g,α,1/VertexCount[g]]に等しい．
  • ページランク中心性は正規化される．
  • オプションWorkingPrecision->p を使って内部計算で使われる精度が制御できる．
  • PageRankCentralityは，無向グラフ，有向グラフ，多重グラフ，混合グラフに使うことができる．

例題

すべて開くすべて閉じる

例  (2)

ページランク中心性を計算する：

ハイライトする：

ランダムにハイパーリンクをクリックした人が特定のページに辿り着く確率を求める：

最も目立つページを先頭にしてWebページを順位付けする：

スコープ  (7)

PageRankCentralityは無向グラフに使うことができる：

有向グラフ：

多重グラフ：

混合グラフ：

規則を使ってグラフを指定する：

デフォルトではない初期中心性：

PageRankCentralityは大きいグラフに使うことができる：

オプション  (3)

WorkingPrecision  (3)

デフォルトで，PageRankCentralityは機械精度計算で中心性を求める：

より高い作業精度を指定する：

無限の作業精度は厳密計算に相当する：

アプリケーション  (6)

ランダムにハイパーリンクをクリックして特定のページに至る尤度に基づいてWebサイトに順位を付ける：

CycleGraphのページランク中心性をハイライトする：

GridGraph：

CompleteKaryTree：

PathGraph：

ある会社のWebページのネットワークがハイパーリンクで繋がれている．減衰係数0.85の場合に多数のクリックの後で辿り着く確率が最も高いページを求める：

ノードが道路を表し，2本の道路が交差している場合はこの2つのノードが連結されている道路のネットワーク．常に交通のある道路を予想する：

絶滅すると食物連鎖の崩壊に至る種を求める：

淋菌の代謝細胞ネットワーク．系の中で周辺機能の役割を果たすタンパク質を求める：

これらのタンパク質の入次数が最も低い：

特性と関係  (3)

中心性ベクトルは線形系 c=alpha TemplateBox[{a}, Transpose].d.c+beta の正規化した解である：

線形系を解く：

ページランク中心性は正規化されている：

VertexIndexを使って特定の頂点の中心性を求める：

Wolfram Research (2010), PageRankCentrality, Wolfram言語関数， https://reference.wolfram.com/language/ref/PageRankCentrality.html （2024年に更新）.

テキスト

Wolfram Research (2010), PageRankCentrality, Wolfram言語関数， https://reference.wolfram.com/language/ref/PageRankCentrality.html （2024年に更新）.

CMS

Wolfram Language. 2010. "PageRankCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/PageRankCentrality.html.

APA

Wolfram Language. (2010). PageRankCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PageRankCentrality.html

BibTeX

@misc{reference.wolfram_2025_pagerankcentrality, author="Wolfram Research", title="{PageRankCentrality}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/PageRankCentrality.html}", note=[Accessed: 03-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_pagerankcentrality, organization={Wolfram Research}, title={PageRankCentrality}, year={2024}, url={https://reference.wolfram.com/language/ref/PageRankCentrality.html}, note=[Accessed: 03-April-2025 ]}