PowerMod

✖
`PowerMod`

✖

PowerMod[a,b,m]

m を法として a^b を与える．

✖

PowerMod[a,-1,m]

m を法とした a の逆モジュロを与える．

✖

PowerMod[a,1/r,m]

a の第 r 根のモジュロを与える．

詳細

PowerModはベキ剰余としても知られている．
数値操作と記号操作の両方に適した数学関数である．
合同算術，暗号学，乱数生成，プログラミングにおける循環作業によく使われる．
PowerMod[a,b,m]は a^bを m で割ったときの余りを与える．

PowerMod[a,b,m]における b の値は負でもよく，有理数でもよい．対応する逆モジュロや根が存在しない場合は未評価で返される．
PowerMod[a,b,m]は，正の b について，Mod[a^b, m]と同じ結果をはるかに効率よく与える．

例題

すべて開くすべて閉じる

例 (3)基本的な使用例

3を法としてを計算する：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-bhvswr

Out[1]=1

数列を固定ベキでプロットする：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-13f5dt

Out[1]=1

数列をベキを変化させてプロットする：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-0anv6y

Out[1]=1

スコープ (7)標準的な使用例のスコープの概要

数値評価 (4)

整数を使って計算する：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-yvd759

Out[1]=1

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-jkq

Out[1]=1

有理指数：

In[6]:=6

✖

https://wolfram.com/xid/0j42dluq-5wzqg8

Out[6]=6

ガウス整数：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-l81a2x

Out[1]=1

大きい数について計算する：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-k3q

Out[1]=1

PowerModはリストに縫い込まれる：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-ubw

Out[1]=1

TraditionalFormによる表示：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-hildxd

記号演算 (3)

Reduceを使って式を簡約する：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-npu0o8

Out[1]=1

FindInstanceを使ってPowerModを含む式の解を求める：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-dg7pul

Out[1]=1

PowerModを総和で使う：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-nd928r

Out[1]=1

アプリケーション (6)この関数で解くことのできる問題の例

基本的なアプリケーション (2)

9のPrimitiveRootを求める：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-iv0

Out[1]=1

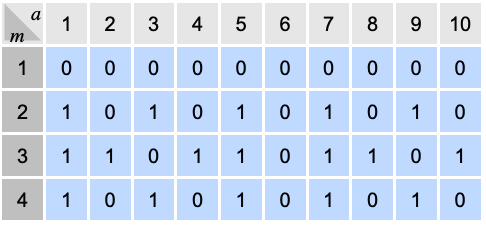
9を法として互いに素なすべての整数を PowerModを使って生成する：

In[2]:=2

✖

https://wolfram.com/xid/0j42dluq-ijkmdx

Out[2]=2

が基底の擬似素数を認識する：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-73ghej

2が基底の1000より小さい擬似整数をすべて求める：

In[2]:=2

✖

https://wolfram.com/xid/0j42dluq-ddotbl

Out[2]=2

5が基底の1000より小さい擬似整数をすべて求める：

In[3]:=3

✖

https://wolfram.com/xid/0j42dluq-v2utbo

Out[3]=3

整数論 (4)

RSAのようなトイ暗号スキームを構築する．法から始める：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-9ow8f9

Out[2]=2

n を法とする乗法群の普遍指数を求める：

In[3]:=3

✖

https://wolfram.com/xid/0j42dluq-6u3x4k

Out[3]=3

秘密鍵：

In[4]:=4

✖

https://wolfram.com/xid/0j42dluq-dqq7e

Out[4]=4

公開鍵：

In[5]:=5

✖

https://wolfram.com/xid/0j42dluq-dphnlq

Out[5]=5

メッセージを暗号化する：

In[6]:=6

✖

https://wolfram.com/xid/0j42dluq-rlww9o

Out[6]=6

それを解読する：

In[7]:=7

✖

https://wolfram.com/xid/0j42dluq-n7ftgl

Out[7]=7

RSAのようなトイ暗号スキームを構築する：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-wi9r7

循環攻撃を行う．出力の1つはテキストである：

In[2]:=2

✖

https://wolfram.com/xid/0j42dluq-eqzmrb

Out[2]=2

アリスとボブは，素数とその素数を法とする原始根に公的に同意する：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-jcibqc

In[2]:=2

✖

https://wolfram.com/xid/0j42dluq-k0fs8w

次に，アリスとボブはそれぞれ秘密鍵を選ぶ：

In[3]:=3

✖

https://wolfram.com/xid/0j42dluq-mgkfzh

次に，アリスはボブにを法とするを送り，ボブはアリスにを法とするを送る：

In[4]:=4

✖

https://wolfram.com/xid/0j42dluq-m69s8l

In[5]:=5

✖

https://wolfram.com/xid/0j42dluq-n3z4dz

次に，ボブはを法とするを計算し，アリスはを法とするを計算する：

In[6]:=6

✖

https://wolfram.com/xid/0j42dluq-h8qnsc

Out[6]=6

In[7]:=7

✖

https://wolfram.com/xid/0j42dluq-stj76g

Out[7]=7

次が，彼らが共有している秘密の数である：

In[8]:=8

✖

https://wolfram.com/xid/0j42dluq-up29yo

Out[8]=8

現行時刻をシードとして使う乱数生成器を作成する：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-qx2pgi

Out[1]=1

法と基底を選ぶ：

In[2]:=2

✖

https://wolfram.com/xid/0j42dluq-kvu9y8

からまでの個の乱数を計算する：

In[3]:=3

✖

https://wolfram.com/xid/0j42dluq-8c5v1l

Out[3]=3

特性と関係 (8)この関数の特性および他の関数との関係

PowerModは周期関数である：

In[2]:=2

✖

https://wolfram.com/xid/0j42dluq-ud8amv

Out[2]=2

Modを使ってPowerModを決定する：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-d8q8jd

Out[1]=1

ModularInverseを決定する：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-o5llde

Out[1]=1

でならである：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-i1dp6y

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0j42dluq-tssupn

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0j42dluq-lqnk95

Out[3]=3

がの除数ならである：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-n4wlj

Out[1]=1

とが互いに素ならである：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-bm3vdo

Out[1]=1

フェルマの小定理にはが素数ならであるとある：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-wuz10w

Out[1]=1

結果は法と同じ符号を持つ：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-mfn

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0j42dluq-di3

Out[2]=2

考えられる問題 (1)よく起る問題と予期しない動作

モジュール式の平方根は存在しないことがある：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-xip

Out[1]=1

おもしろい例題 (3)驚くような使用例や興味深い使用例

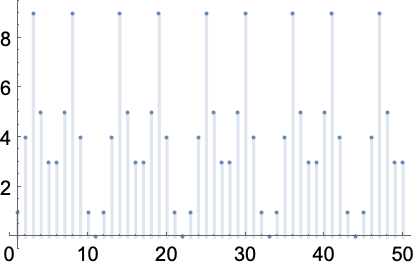
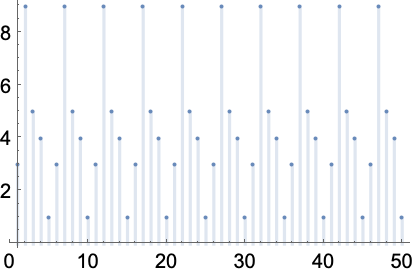
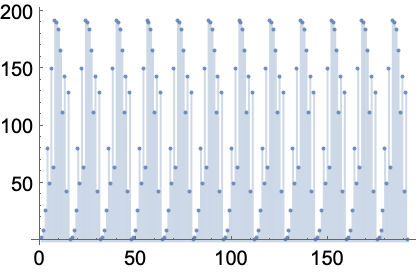
指数が変化するときに，ある素数を法とする3のベキ乗のリストをプロットする：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-g430z5

Out[1]=1

固定の法で数のさまざまなベキの値をプロットする：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-h1vfz5

Out[1]=1

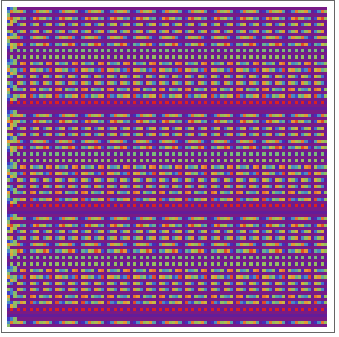
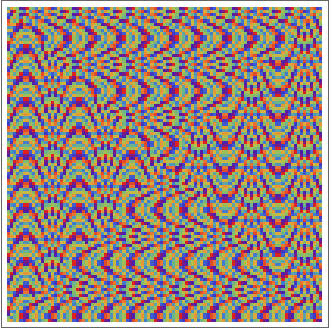
PowerModに基づいて数が彩色されたウラム(Ulam)の螺線をプロットする：

In[1]:=1

✖

https://wolfram.com/xid/0j42dluq-gsvx6n

Out[1]=1

トップへ