gives the Riemann–Siegel function ![]() .
.


RiemannSiegelTheta
gives the Riemann–Siegel function ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
![TemplateBox[{t}, RiemannSiegelTheta]=Im(TemplateBox[{{{1, /, 4}, +, {{(, {ⅈ, , t}, )}, /, 2}}}, LogGamma])-t/2log pi TemplateBox[{t}, RiemannSiegelTheta]=Im(TemplateBox[{{{1, /, 4}, +, {{(, {ⅈ, , t}, )}, /, 2}}}, LogGamma])-t/2log pi](Files/RiemannSiegelTheta.en/2.png) for real
for real 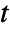 .
. ![TemplateBox[{t}, RiemannSiegelTheta] TemplateBox[{t}, RiemannSiegelTheta]](Files/RiemannSiegelTheta.en/4.png) arises in the study of the Riemann zeta function on the critical line. It is closely related to the number of zeros of
arises in the study of the Riemann zeta function on the critical line. It is closely related to the number of zeros of ![TemplateBox[{{{1, /, 2}, +, {ⅈ, , u}}}, Zeta] TemplateBox[{{{1, /, 2}, +, {ⅈ, , u}}}, Zeta]](Files/RiemannSiegelTheta.en/5.png) for
for 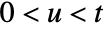 .
. ![TemplateBox[{t}, RiemannSiegelTheta] TemplateBox[{t}, RiemannSiegelTheta]](Files/RiemannSiegelTheta.en/7.png) is an analytic function of
is an analytic function of 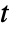 except for branch cuts on the imaginary axis running from
except for branch cuts on the imaginary axis running from 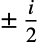 to
to 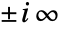 .
. - For certain special arguments, RiemannSiegelTheta automatically evaluates to exact values.
- RiemannSiegelTheta can be evaluated to arbitrary numerical precision.
- RiemannSiegelTheta automatically threads over lists.
- RiemannSiegelTheta can be used with Interval and CenteredInterval objects. »
Examples
open all close allBasic Examples (6)
Plot over a subset of the reals:
Plot over a subset of the complexes:
Series expansion at the origin:
Series expansion at Infinity:
Scope (28)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix RiemannSiegelTheta function using MatrixFunction:
Specific Values (2)
Visualization (2)
Plot the RiemannSiegelTheta:
Plot the real part of the RiemannSiegelTheta function:
Plot the imaginary part of the RiemannSiegelTheta function:
Function Properties (11)
RiemannSiegelTheta is defined for all real values:
Function range of RiemannSiegelTheta:
RiemannSiegelTheta threads elementwise over lists:
RiemannSiegelTheta is an analytic function of x:
RiemannSiegelTheta is non-increasing in a specific range:
RiemannSiegelTheta is not injective:
RiemannSiegelTheta is surjective:
RiemannSiegelTheta is neither non-negative nor non-positive:
RiemannSiegelTheta has no singularities or discontinuities:
RiemannSiegelTheta is neither convex nor concave:
TraditionalForm formatting:
Differentiation (3)
Generalizations & Extensions (2)
Applications (3)
Plot real and imaginary parts over the complex plane:
Show interlacing of the roots of Sin[RiemannSiegelTheta[t]] and RiemannSiegelZ[t]:
Compute Gram points:
Show good Gram points, where RiemannSiegelZ changes sign for consecutive points:
Properties & Relations (3)
RiemannSiegelTheta is related to LogGamma:
RiemannSiegelZ can be expressed in terms of RiemannSiegelTheta and Zeta:
Possible Issues (2)
A larger setting for $MaxExtraPrecision might be needed:

Neat Examples (1)
Riemann surface of RiemannSiegelTheta:
See Also
Tech Notes
Related Guides
Related Links
History
Introduced in 1991 (2.0) | Updated in 2023 (13.3)
Text
Wolfram Research (1991), RiemannSiegelTheta, Wolfram Language function, https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html (updated 2023).
CMS
Wolfram Language. 1991. "RiemannSiegelTheta." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html.
APA
Wolfram Language. (1991). RiemannSiegelTheta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html
BibTeX
@misc{reference.wolfram_2025_riemannsiegeltheta, author="Wolfram Research", title="{RiemannSiegelTheta}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_riemannsiegeltheta, organization={Wolfram Research}, title={RiemannSiegelTheta}, year={2023}, url={https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html}, note=[Accessed: 09-March-2026]}