SignedRegionDistance
SignedRegionDistance[reg,p]
如果 p 位于区域外,给出从点 p 到区域 reg 的最小距离;如果 p 位于区域内,给出到 reg 的补集的最小距离.
SignedRegionDistance[reg]
给出 RegionDistanceFunction[…],可以重复应用于不同的点.
更多信息和选项

- SignedRegionDistance 也称为有符号距离函数和有符号距离变换.
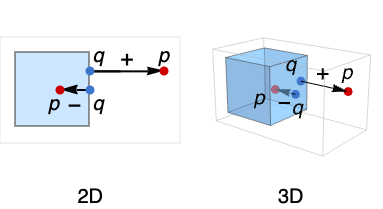
- 对于区域外的点,SignedRegionDistance 为正,对于区域内的点则为负. 绝对值测量的是点与边界的接近程度.
- 点 q 和 p 之间的距离是 Norm[p-q].
- SignedRegionDistance 实际上是 MinValue[{Norm[p-q],q∈reg},q∈reg],当 p 不在 reg 中,并且满足-MinValue[{Norm[p-q],q∉reg},q].
- SignedRegionDistance 可被用于 GeometricScene 中的符号区域和点.
范例
打开所有单元关闭所有单元基本范例 (2)
求从一个点到 MeshRegion 的符号距离:
在一个参数下,您得到 RegionDistanceFunction:
范围 (17)
特殊区域 (8)
公式区域 (2)
网格区域 (4)
BoundaryMeshRegion 的符号距离在任意维度可以是负的:
符号距离在一维空间中不可以是相对于零维 MeshRegion 的负值:
但是对于一维 MeshRegion,它可以:
在二维中,对于 0D MeshRegion 带符号的距离不可以为负:
对于一维 MeshRegion,不可以:
但是对于二维 MeshRegion,它可以:
符号距离在三维空间中不可以是相对于零维 MeshRegion 的负值:
对于一维 MeshRegion,不可以:
对于二维 MeshRegion,不可以:
但是对于三维 MeshRegion,它就可以:
导出区域 (3)
应用 (2)
属性和关系 (5)
一个点是 RegionMember,如果区域的符号距离是非正的:
RegionBoundary 上的一个点具有符号的距离0:
SignedRegionDistance 的 Abs 是到 RegionBoundary 的距离的 MinValue:
对于区域外的一个点,RegionDistance 和 SignedRegionDistance 是相同:
文本
Wolfram Research (2014),SignedRegionDistance,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SignedRegionDistance.html.
CMS
Wolfram 语言. 2014. "SignedRegionDistance." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SignedRegionDistance.html.
APA
Wolfram 语言. (2014). SignedRegionDistance. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SignedRegionDistance.html 年