SmoothKernelDistribution

SmoothKernelDistribution[{x1,x2,…}]

データ値 xiに基づいた平滑化カーネル分布を表す．

SmoothKernelDistribution[{{x1,y1,…},{x2,y2,…},…}]

データ値{xi,yi,…}に基づいた多変量平滑化カーネル分布を表す．

SmoothKernelDistribution[…,bw]

帯域幅 bw の平滑化カーネル分布を表す．

SmoothKernelDistribution[…,bw,ker]

帯域幅 bw，平滑化カーネル ker の平滑化カーネル分布を表す．

詳細とオプション

  • SmoothKernelDistributionは他の任意の確率分布とも同じように使えるDataDistributionオブジェクトを返す．
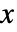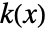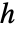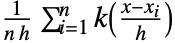  • SmoothKernelDistributionの値 についての確率密度関数は，平滑化カーネル と帯域幅母数 についての線形補間バージョンで与えられる．
  • 帯域幅 bw の可能な指定値
  • h使用する帯域幅
    {"Standardized",h}標準偏差の単位による帯域幅
    {"Adaptive",h,s}初期帯域幅 h，感度 s で適応的
    Automatic自動計算された帯域幅
    "name"名前付き帯域幅選択法を使う
    {bwx,bwy,…}x, y 等に別々の帯域幅指定
  • 多変量密度については，h は正定対称行列でもよい．
  • 適応的帯域幅については，感度 s は0から1までの実数あるいはAutomaticでなければならない．Automaticの場合，s は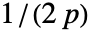に設定される．ただし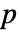， はデータの次元である．
  • 使用可能な名前付き帯域幅選択メソッド
  • "LeastSquaresCrossValidation"最小二乗クロス確認法を使う
    "Oversmooth"標準Gaussianの1.08倍広い
    "Scott"Scottの規則を使った帯域幅選択
    "SheatherJones"Sheather–Jonesプラグイン推定器を使う
    "Silverman"Silvermanの規則を使った帯域幅の決定
    "StandardDeviation"帯域幅として標準偏差を使う
    "StandardGaussian"標準正規データの最適帯域幅
  • デフォルトで"Silverman"メソッドが使われる．
  • 自動帯域幅計算では，定配列は単位分散を持つとみなされる．
  • 次のカーネル指定 ker が使える．
  • "Biweight"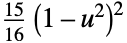
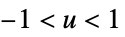
    "Cosine"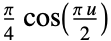
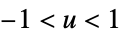
    "Epanechnikov"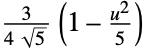
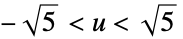
    "Gaussian"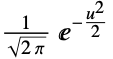
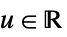
    "Rectangular"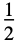
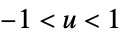
    "SemiCircle"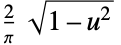
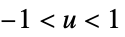
    "Triangular"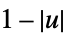
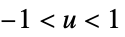
    "Triweight"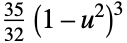
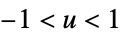
    func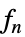f_nu in R
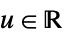
  • SmoothKernelDistributionが真の密度推定を生成するためには，関数 fn が有効な確率密度関数でなければならない．
  • デフォルトで，"Gaussian"カーネルが使われる．
  • カーネル関数 ker を指定し，{"Bounded",c,ker}を使ってもとになっている密度の既知の境界を構成することができる．ただし，c は任意の実数，c1<c2であるリスト{c1,c2}，あるいは長さが data の次元と等しいリスト{{c11,c12},{c21,c22},…}でよい．
  • 多変量密度については，{"Product",ker}と{"Radial",ker}を使ってカーネル関数 ker をそれぞれ積およびラジアルのタイプとして指定することができる．タイプの指定がない場合は積タイプのカーネルが使われる．
  • 密度推定に用いられる精度は bw とデータで与えられる最低精度である．
  • 使用可能なオプション
  • InterpolationPoints Automatic使用する初期補間点の数
    MaxMixtureKernels Automatic使用するカーネルの最大数
    MaxRecursion Automatic許容する再帰下位区分の数
    PerformanceGoal Automaticスピードまたは品質の最適化
    MaxExtraBandwidths Automatic使用するデータの範囲を超える最大帯域幅
  • SmoothKernelDistributionはMean，CDF，RandomVariate等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (2)

一変量データについてカーネル密度推定の補間されたバージョンを作成する：

結果の分布を使って分布関数の可視化を含む分析を行う：

モーメントと分位数を計算する：

二変量データについてカーネル密度推定の補間されたバージョンを作成する：

推定された確率密度関数と累積分布関数を可視化する：

共分散と一般化されたモーメントを計算する：

スコープ  (37)

基本的な用法  (7)

あるデータの補間された平滑な密度推定を作成する：

分布から確率を計算する：

単位付きの数量についての外挿版カーネル密度推定を作る：

モーメントを求める：

より滑らかな推定を得るために帯域幅を大きくする：

局所密度によって帯域幅が適応的に変更されるようにする：

より高次元でカーネル密度推定量を補間する：

一変量周辺確率密度関数をプロットする：

二変量周辺確率密度関数をプロットする：

組込みのカーネル関数から選択する．あるいはカスタム関数を構築する：

カスタムカーネル関数：

多変量の推定のためにラジアルタイプカーネルか積タイプカーネルを指定する：

分布特性  (8)

分布関数を推定する：

分布のモーメントを計算する：

特殊なモーメント：

一般的なモーメント：

分位関数：

特殊な分位値：

乱数を生成する：

SmoothKernelDistributionと比較する：

確率と期待値を計算する：

二変量分布関数を推定する：

二変量分布のモーメントを計算する：

特殊なモーメント：

一般的なモーメント：

乱数を生成する：

点分布を示す：

帯域幅の選択  (12)

使用する帯域幅を自動的に選ぶ：

データが多い程もとになっている分布がうまく近似できる：

帯域幅を明示的に指定する：

0.1と1の帯域幅を使う：

帯域幅が広い程滑らかな推定になる：

帯域幅を標準偏差の単位で指定する：

標準偏差の と の帯域幅を使う：

局所密度に従って適応的に帯域幅が変えられるようにする：

局所感度を0 (none)から1(full)に変える：

適応的推定値についての初期帯域幅を変化させる：

初期帯域幅をそれぞれ1.0と0.1に指定する：

いくつかの自動帯域幅選択メソッドのうち任意のものを使う：

デフォルトでSilvermanのメソッドが使われる：

確率密度関数は等値である：

デフォルトで，各次元の帯域幅を別々に選ぶのにSilvermanのメソッドが使われる：

任意の自動メソッドを使って帯域幅の対角要素を別々に選ぶことができる：

帯域幅の対角の推定に使われるメソッドは同じではなくてもよい：

適応的な帯域幅，過度に平滑化された帯域幅，一定の帯域幅をそれぞれの次元に使う：

一変量周辺確率密度関数をプロットする：

すべての次元で同じ帯域幅を使うためにスカラー値を与える：

非零の対角外要素を使うために，完全に指定された帯域幅行列を与える：

カーネル関数  (6)

いくつかのカーネル関数から任意のものを指定する：

カーネル関数を純関数として定義する：

デフォルトで，ガウスカーネルが使われる：

これはNormalDistribution[0,1]の確率密度関数を使うのに等しい：

いくつかの一変量カーネル関数の形：

多変量データのためにいくつかのカーネル関数から任意のものを指定する：

多変量データのために積タイプカーネル関数とラジアルタイプカーネル関数のいずれかを選ぶ：

固定領域における推定  (4)

領域内に留まるように境界を使う：

ガウスカーネルで平滑化カーネル分布を定義する：

偏微分方程式についてのサポートはデータについてのサポートを超える：

境界を強制する：

もとのBetaDistributionと比較する：

平滑化カーネル分布を有界Epanechnikovカーネルと比較する：

有界平滑化カーネル密度推定は，境界付近でより正確である：

二次元データに有界余弦カーネルを使う：

推定密度を人口分布密度と比較する：

有界ガウスカーネル：

通常の平滑化カーネル分布を切断すると，違った結果になる：

オプション  (25)

InterpolationPoints  (6)

デフォルトで，滑らかな推定を得るために非一様補間が使われる：

使用するサンプル点の初期数を指定する：

4つの補間点を使う：

点の数が多い程推定は滑らかになる：

二変量データで使用する補間点の数を指定する：

各次元で5個と50個の補間点を使う：

各次元で異なる数の補間点を使う：

3と30あるいは30と3の点を指定する：

滑らかな結果が高品質の推定を保証するものではない：

この場合は1000の補間点を使って非常に滑らかな推定を行う：

MaxExtraBandwidths  (6)

デフォルトで，推定は最高でデータを12帯域幅分超える：

使用する最大帯域幅数を指定する：

0帯域幅と12帯域幅をそれぞれ使う：

各端点に異なる数を設定する：

多変量データで使用する予備の帯域幅数を指定する：

0と12の帯域幅をそれぞれ使用する：

各次元で使用する予備の帯域幅数を指定する：

0と12あるいは12と0の帯域幅をそれぞれ使用する：

各次元の各端点に異なる数を設定する：

MaxMixtureKernels  (6)

デフォルトで，カーネル数は一般に最適化されている：

推定で使うカーネルの最大数を指定する：

最大で5つのカーネルを置く：

カーネルの数が多い程もとになっている分布がうまく推定できる：

各データ点にカーネルを置く：

同数のカーネルで使われる帯域幅を変える：

二変量データの各次元で使用されるカーネルの最大数を指定する：

それぞれ最高で10と100のカーネルを置く：

各次元の最大カーネル数を設定する：

最大でそれぞれ5と50あるいは50と5のカーネルを指定する：

MaxRecursion  (4)

デフォルトで普通は滑らかな推定が返される：

使用する再帰的再分割の最大数を指定する：

二変量データの再帰的再分割の最大数を与える：

最高でそれぞれ2回と6回の再分割を行う：

各次元の再帰的再分割の最大数を設定する：

最大再分割数を0と3あるいは3と0に指定する：

PerformanceGoal  (3)

デフォルトで，推定はスピードと品質の間でバランスを取って最適化されている：

スピードあるいは品質のPerformanceGoalを設定するか，Automaticを使って両者のバランスを取る：

PerformanceGoalを"Quality"に設定するとより時間がかかる：

ControlActiveと一緒に使ってPerformanceGoalを動的に変える：

アプリケーション  (14)

推定密度を理論モデルと比較する：

高度に振動する密度に適応的帯域幅を使う：

モデルのモーメントと推定は似ている：

TruncatedDistributionを使って平滑化の後の領域を限定する：

推定は正の値に限定されている：

分布が切断範囲を境界としていることを確かめる：

Casesと一緒に使って平滑化の前のデータ領域を限定する：

推定は左側ではデータを超えるがデータは正の値に限定されている：

データが0より下になる確率は0ではない：

MaxExtraBandwidthsを使ってデータを落とすことなく領域を限定する：

推定は最小のデータ値（正に限定）で停止する：

ヒト染色体の長さの分布を推定する：

長さが平均より長いとした場合に，期待される染色体の長さ：

連続する素数の差の離散分布を平滑化する：

1990年代におけるS&P 500の日々の配当の差の分布を調べる：

平滑化された分布とフィットされたモデルを比べる：

大学の2つの学部の給与分布を比較する：

2つの学部の給与を選択し，通貨単位を加える：

オールド・フェイスフルの噴出時間と次の噴出までの待ち時間の結合分布を推定する：

噴出が2分より長く続き，待ち時間が1時間より短い確率：

ヒストグラムを平滑化する：

平滑化のためにヒストグラムから乱数を生成する：

SurvivalDistributionから返された推定を平滑化する：

生存時間が10より大きいとして25を超える生存確率を計算する：

ニューヨーク州バッファローにおける積雪量の確率密度関数の信頼帯を作る：

各ブートストラップサンプルを平滑化し，信頼推定を得る：

95%の信頼帯で確率密度関数の推定を可視化する：

p 次元多変量正規データを仮定して，マハラノビス(Mahalanobis)距離が漸近的ChiSquareDistribution[p]であることを確認する：

四次元正規データを仮定した場合のマハラノビス距離が10を超える確率：

パラメトリック裾部モデルを使って裾部が重い密度を推定する：

本体はうまく推定されるが，データが少ないために裾部はあまり平滑化されていない：

カーネル密度推定と推定裾部モデルの混合を作る：

推定全体が平滑化されている：

特性と関係  (8)

結果の密度推定を積分すると単位元になる：

デフォルトで，機械推定が使われる：

高精度データを使って高精度の推定を得る：

確率密度関数は区分的に一次である：

累積分布関数とSurvivalFunctionは区分的に二次である：

HazardFunctionは二次よりも一次で区分的に有理である：

SmoothKernelDistributionはもとになっている分布を一貫して推定する：

帯域幅が無限大に近付くにつれ，推定はカーネルの形に近付く：

SmoothKernelDistributionはKernelMixtureDistributionの線形補間である：

SmoothKernelDistributionは，入力がTimeSeriesまたはEventSeriesのときのみ値に使うことができる：

以下と同じである：

SmoothKernelDistributionは，入力がTemporalDataのときは，すべての値に同時に働く：

以下と同じである：

考えられる問題  (4)

カーネル関数は確率密度関数である必要がある：

結果の密度推定は確率密度関数ではない：

自動的に適応される帯域幅は，大きいサンプルには小さすぎるかもしれない：

初期帯域幅かMaxMixtureKernelsを大きくするか，感度を小さくするかする：

SmoothKernelDistributionはもとになっている分布の領域を知らない：

もとになっている分布は離散的であるが，推定された確率密度関数は連続的である：

推定された確率密度関数はで有界ではない：

重度に適応的な帯域幅の場合，これらの問題はそれほど明らかではない：

分布の中には裾部が重過ぎて効果的に補間できないものもある：

KernelMixtureDistributionは補間に依存しない記号的なメソッドを使う：

おもしろい例題  (2)

現在地近くの気温分布を計算する：

西ウガンダの火山クレーターの密度を推定する：

回転数を使った外接多角形の領域関数：

Wolfram Research (2010), SmoothKernelDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), SmoothKernelDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "SmoothKernelDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html.

APA

Wolfram Language. (2010). SmoothKernelDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html

BibTeX

@misc{reference.wolfram_2024_smoothkerneldistribution, author="Wolfram Research", title="{SmoothKernelDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_smoothkerneldistribution, organization={Wolfram Research}, title={SmoothKernelDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html}, note=[Accessed: 21-November-2024 ]}