SmoothKernelDistribution

SmoothKernelDistribution[{x1,x2,…}]

表示基于数据值 xi 的平滑核分布.

SmoothKernelDistribution[{{x1,y1,…},{x2,y2,…},…}]

表示基于数据值 {xi,yi,…} 的多元平滑核分布.

SmoothKernelDistribution[…,bw]

表示带宽为 bw 的平滑核分布.

SmoothKernelDistribution[…,bw,ker]

表示带宽为 bw 以及平滑核为 ker 的平滑核分布.

更多信息和选项

  • SmoothKernelDistribution 返回一个可以像任何其它概率分布一样使用的 DataDistribution 对象.
  • 一个值 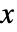的 SmoothKernelDistribution 的概率密度函数由平滑核 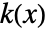和带宽参数 的 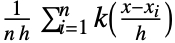的线性插值版本给出.
  • 可以给出如下带宽说明 bw：
  • h要使用的带宽
    {"Standardized",h}以标准差为单位的带宽
    {"Adaptive",h,s}具有初始带宽 h 和灵敏度 s 的自适应性
    Automatic自动计算的带宽
    "name"使用一个已命名的带宽选择方法
    {bwx,bwy,…}对 x、y 等的不同的带宽说明
  • 对于多变量密度，h 可以是正定对称矩阵.
  • 对于自适应带宽，敏感度 s 必须是介于0和1之间的实数或 Automatic. 如果使用 Automatic，s 被设为 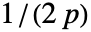，其中 是数据的维数.
  • 可能的已命名带宽选择方法包括：
  • "LeastSquaresCrossValidation"使用最小二乘交叉核实法
    "Oversmooth"比标准高斯宽1.08倍
    "Scott"使用 Scott 规则来确定带宽
    "SheatherJones"使用 Sheather-Jones 插入式估计量
    "Silverman"使用 Silverman 规则来确定带宽
    "StandardDeviation"使用标准差作为带宽
    "StandardGaussian"标准正态数据的最佳带宽
  • 默认使用 "Silverman" 法.
  • 对于自动带宽计算，假定常量数组具有单位方差.
  • 可以给出的可能的核说明 ker 有：
  • "Biweight"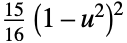
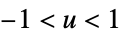
    "Cosine"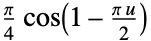
    "Epanechnikov"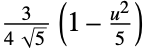
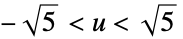
    "Gaussian"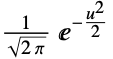
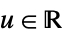
    "Rectangular"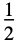
    "SemiCircle"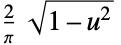
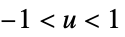
    "Triangular"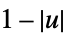
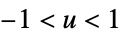
    "Triweight"
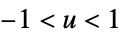
    funcf_nu in R
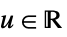
  • 为了使 SmoothKernelDistribution 能够生成一个真正的密度估计，函数 fn 应该是一个有效的概率密度函数.
  • 默认使用 "Gaussian" 核.
  • 内核函数 ker 可以使用 {"Bounded",c,ker} 指定来考虑内在密度的已知边界，其中 c 可以是任意实数、列表 {c1,c2} 满足 c1<c2，或者列表 {{c11,c12},{c21,c22},…}，其中长度等于 data 的维度.
  • 对于多变量密度，核函数 ker 可以分别使用 {"Product",ker} 和 {"Radial",ker} 指定 Product 和 Radial 类型. 如果没有指定类型，则使用 Product 类型核.
  • 密度估计所用的精度是在 bw 和数据中给出的最小精度.
  • 可以给出以下选项：
  • InterpolationPoints Automatic所使用的插值点的初始数目
    MaxMixtureKernels Automatic所使用的核的最大数目
    MaxRecursion Automatic所允许的递归细分数目
    PerformanceGoal Automatic对速度或者质量进行优化
    MaxExtraBandwidths Automatic超过要使用的数据的最大带宽
  • SmoothKernelDistribution 可以与诸如 Mean、CDF 和 RandomVariate 等函数一起使用.

范例

打开所有单元关闭所有单元

基本范例  (2)

创建单变量数据的一个核密度估计的内插版本：

使用所得到的分布来执行分析，包括将分布函数可视化：

计算矩和分位数：

创建一些二元数据的核密度估计的内插版本：

将估计的概率密度函数和累计分布函数可视化：

计算协方差和一般矩：

范围  (37)

基本用途  (7)

创建对一些数据的内插平滑密度估计：

计算分布的概率：

创建带有数量的数据的核密度估计的插值版本：

求矩：

增加带宽以便更平滑的估计：

允许根据局部密度自适应变化带宽：

在更高维数中内插核密度估计：

绘制一元边缘概率密度函数：

绘制二元边缘概率密度函数：

从内置核函数中选择或自定义一个：

自定义核函数：

为多元估计指定径向或乘积类型核：

分布属性  (8)

估计分布函数：

计算分布的矩：

特色矩：

一般矩：

分位数函数：

特定的分位数值：

生成随机数：

与 SmoothKernelDistribution 比较：

计算概率和期望值：

估计二元概率函数：

计算二元分布的矩：

特殊矩：

一般矩：

产生随机数：

显示点分布：

带宽选择  (12)

自动选择使用的带宽：

对于基本的分布，更多的数据产生更好的近似：

明确指定使用的带宽：

使用 0.1 和 1 带宽：

更大的带宽产生更平滑的估计：

以标准差单位指定带宽：

使用标准差的 和 为带宽：

允许带宽随局部密度自适应变动：

从0（无）到 1（全）变动局部敏感度：

为自适应估计变动初始带宽：

分别指定 1.0 和 0.1 为初始带宽：

使用多个自动带宽选择方法中的任一个：

默认情况下，使用 Silverman 方法：

概率密度函数是相等的：

默认情况下，使用 Silverman 方法在每一方向上独立选择带宽：

可以使用任何自动的方法独立选择对角线带宽元素：

用于估计带宽对角线的方法没有必要一样：

在各个维度上使用自适应、过平滑和常量带宽：

绘制一元边缘概率密度函数：

给出标量值以便在所有维度上使用同样的带宽：

为了使用非零非对角线元素，给出完全指定的带宽矩阵：

核函数  (6)

指定多个核函数中的任意一个：

定义核函数为一个纯函数：

默认情况下，使用高斯核：

这等同于使用 NormalDistribution[0,1] 的概率密度函数：

一些一元核函数的形状：

对多元数据指定多个核函数中的任意一个：

在多元数据的积与径向类型的核函数间选择：

使用固定域估计  (4)

使用边界位于域范围内：

定义具有高斯核的平滑核分布：

对 PDF 的支持超过数据支持的范围：

强加边界：

与原始 BetaDistribution 比较：

比较平滑核分布和有界 Epanechnikov 核：

有界平滑核密度估计在边界上更准确：

对二维数据使用一个有界余弦内核：

将估计密度与总体分布密度比较：

有界高斯内核：

截断普通平滑内核分布将产生一个不同的结果：

选项  (25)

InterpolationPoints  (6)

默认情况下，非均匀插值用于创建一个平滑估计量：

指定要使用的样本点的初始数目：

使用4个插值点：

较多的点产生较平滑的估计量：

指定二元数据所用的插值点的数目：

在每个维度上使用5和50个插值点：

在每个维度上，使用不同数目的插值点：

指定3和30个点或者30和3：

一个平滑结果不意味着一个高质量的估计量：

在这种情况下，使用1000个插值点创建了一个非平滑的估计量：

MaxExtraBandwidths  (6)

默认情况下，估计量在数据之外延伸了12个带宽：

设置要使用的带宽的最大数目：

分别使用0和12个带宽：

对每个端点，设置一个不同的数目：

指定多元数据所用的额外带宽的数目：

分别使用0和12个带宽：

指定每个维度上所使用的额外带宽的数目：

分别使用0和12个带宽或者12和0个带宽：

对每个维度上的每个端点，设置一个不同的数目：

MaxMixtureKernels  (6)

默认情况下，核的数目通常是最佳的：

指定估计量中使用的核的最大数目：

最多放置5个核：

核的较大数目给出内在分布的较好的估计量：

在每个数据点放置一个核：

改变相同数目的核所用的带宽：

指定对二元数据的每个维度上所用的核的最大数目：

分别放置最多 和 个核：

设置每个维度上核的最大数目：

指定一个5和50个核或者50和5个核的最大值：

MaxRecursion  (4)

默认情况下，一个平滑估计量将被返回：

指定要使用的递归细分的最大数目：

对双变量数据，给出递归细分的最大数目：

分别使用至多2个和6个细分：

在每个维度上，设置递归细分的最大数目：

指定0和3个细分或者3和0个细分的最大值：

PerformanceGoal  (3)

默认情况下，将估计量针对速度与质量进行优化：

对速度或者质量，设置 PerformanceGoal，或使用 Automatic 平衡两者：

在 PerformanceGoal 设置为 "Quality" 时，需要更多时间：

使用 ControlActive 动态变化 PerformanceGoal：

应用  (14)

比较一个估计密度和一个理论模型：

对高度振荡的密度，使用自适应性带宽：

模型的矩和估计量相似：

使用 TruncatedDistribution 来限制平滑后的域：

估计量限制在正值：

验证分布受截断区域约束：

使用 Cases 来限制平滑前的数据域：

估计量超出左边的数据，但是数据限制在正值：

数据降到0以下的概率不是0：

使用 MaxExtraBandwidths 无需删除数据来限制域：

估计在最小数据值中停止，其限于正值：

估计人类染色体长度的分布：

在长度超过均值的情况下，期望的染色体长度：

平滑连续质数的差值的离散分布：

调查九十年代 S&P500 的有差异的日收益分布：

比较平滑分布和拟合模型：

比较大学中两个系的工资分布：

选择两个系的工资并加上货币单位：

估计 Old Faithful 喷泉持续时间和等待时间的联合分布：

一次喷发持续时间大于2分钟，等待时间小于1小时的概率：

对一个直方图进行平滑处理：

从直方图生成随机数以进行平滑处理：

平滑由 SurvivalDistribution 返回一个估计量：

计算在给定生存时间大于 的情况下，生存大于 的概率：

对纽约布法罗的降雪累积量的 PDF，创建一个置信带：

在每个经过自举法处理（bootstrapped）的样本上，进行平滑处理，并且获取置信估计量：

将具有 95% 置信带的 PDF 可视化：

给定 p 维多变量正态数据下，确认 Mahalanobis 距离遵从一个渐进的 ChiSquareDistribution[p]：

给定四维正态数据的情况下，Mahalanobis 距离超过 的概率:

使用参数尾模型估计重尾密度：

整体估计不错，但是由于缺乏数据尾部稍欠平滑：

创建一个核密度估计和估计尾模型的混合：

整个估计是平滑的：

属性和关系  (8)

所得密度估计量的积分为1：

默认情况下，使用机器估计量：

使用高精度数据以获取高精度估计量：

PDF 是分段线性的：

CDF 和 SurvivalFunction 是分段二次的：

在二次上线性的情况下，HazardFunction 是有理分段的：

SmoothKernelDistribution 是内在分布的一个一致的估计量：

在带宽接近无穷大的情况下，估计量核的形状：

SmoothKernelDistribution 是 KernelMixtureDistribution 的一个线性插值：

SmoothKernelDistribution 只在输入为 TimeSeries 或 EventSeries 时才作用于数值：

与之相同的：

SmoothKernelDistribution 当输入是 TemporalData 时作用于所有数值：

与之相同的：

可能存在的问题  (4)

核函数必须是一个 PDF：

所得的密度估计量不是一个 PDF：

在大样本量的情况下，自动自适应性带宽可能太小：

尝试增加初始带宽，MaxMixtureKernels，或者降低灵敏度：

SmoothKernelDistribution 并不知道内在分布的域：

虽然内在的分布是离散的，估计的 PDF 是连续的：

估计的 PDF 在 上不是有界的：

使用自适应性高的带宽，这些问题可能较为不明显：

一些分布的尾部太重，无法有效插值：

KernelMixtureDistribution 使用不依赖于插值的符号式方法：

巧妙范例  (2)

计算您所在位置附近的温度读数的分布：

估计乌干达西部火山口的密度：

使用卷绕数的边界多边形的区域函数：

Wolfram Research (2010)，SmoothKernelDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html （更新于 2016 年）.

文本

Wolfram Research (2010)，SmoothKernelDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html （更新于 2016 年）.

CMS

Wolfram 语言. 2010. "SmoothKernelDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html.

APA

Wolfram 语言. (2010). SmoothKernelDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html 年

BibTeX

@misc{reference.wolfram_2024_smoothkerneldistribution, author="Wolfram Research", title="{SmoothKernelDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_smoothkerneldistribution, organization={Wolfram Research}, title={SmoothKernelDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/SmoothKernelDistribution.html}, note=[Accessed: 21-November-2024 ]}