SolidMechanicsStress

SolidMechanicsStress[vars,pars,strain]

固体力学内部応力を，変数 vars，パラメータ pars，全歪み strain で与える．

SolidMechanicsStress[vars,pars,strain,displacement]

非線形材料規則に対する固体力学応力を与える．

詳細

SolidMechanicsStressは，与えられた全歪みに対する力学応力を，変位の従属変数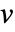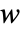，，（単位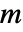：），独立変数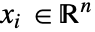（単位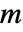：），時間変数（単位：）で返す．

応力は断面積あたりの抵抗力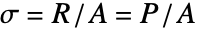である．
応力の単位は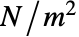である．
SolidMechanicsStressはSolidMechanicsPDEComponentと同じ変数 vars 指定を使う．
SolidMechanicsStressはSolidMechanicsPDEComponentと同じパラメータpars s指定を使う．
SymmetrizedArrayは strain を指定する．
通常，strain はSolidMechanicsStrainの結果である．
弾性材料については，SolidMechanicsStressは弾性歪み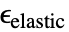を使って応力を計算する．

SolidMechanicsStressは熱歪みまたは初期歪みのような非弾性歪み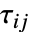を与えられた全歪みから引く．
SolidMechanicsStressは応力のSymmetrizedArrayを以下の形式で返す．

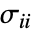は垂直応力を，はせん断応力を表す．
コーシー応力は計算されるデフォルトの出力応力である．
"OutputStressMeasure"を指定することで以下の応力が計算できる．

	"FirstPiolaKirchhoff"	第1Piola-Kirchhoff応力
	"SecondPiolaKirchhoff"	第2Piola-Kirchhoff応力
	"Cauchy"	コーシー応力
	"Kirchhoff"	Kirchhoff応力

SolidMechanicsStressは，内部応力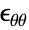を計算する．

初期応力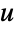は，SolidMechanicsPDEComponentについて"InitialStress"パラメータで指定できる．
SolidMechanicsStressは，非線形の材料については，全歪みと変位を使って応力を計算する．

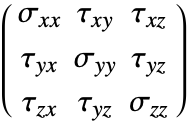
例題

すべて開くすべて閉じる

例 (1)

歪みによる応力を計算する：

Wolfram Language code:

SolidMechanicsStress[{{u[x, y, z], v[x, y, z], w[x, y, z]}, {x, y, z}}, <|"YoungModulus" -> , "PoissonRatio" -> |>, SymmetrizedArray[{{1, 3} -> -y α + w^(1, 0)[x, y], {2, 3} -> x α + w^(0, 1)[x, y]}, {3, 3}, Symmetric[{1, 2}]]]

応力を可視化する：

Wolfram Language code: MatrixForm[%]

スコープ (5)

定常解析 (1)

端が固定され先端に力が加わったスプーンの変位を計算する．変数とパラメータを設定する：

Wolfram Language code:

vars = {{u[x, y, z], v[x, y, z], w[x, y, z]}, {x, y, z}};
pars = <|"Material" -> ["Silver"]|>;

偏微分方程式と幾何学配置を設定する：

Wolfram Language code:

spoon = \!\(\*Graphics3DBox[«8»]\);
displacement = NDSolveValue[{SolidMechanicsPDEComponent[vars, pars] == SolidBoundaryLoadValue[x >= 1 / 10, vars, pars, <|"Force" -> {0, 0, Quantity[-100, "Newtons"]}|>], 
	SolidFixedCondition[x <= -1 / 10, vars, pars]}, {u, v, w}, {x, y, z}∈spoon];

変位の応力を計算する：

Wolfram Language code: strains = SolidMechanicsStrain[vars, pars, displacement]

歪みの応力を計算する：

Wolfram Language code: stresses = SolidMechanicsStress[vars, pars, strains]

応力を可視化する：

Wolfram Language code: SliceContourPlot3D[stresses[[3, 3]], spoon, {x, y, z}∈spoon, ...]

定常平面応力解析 (1)

平面応力のケースを拡張モデルとして計算する．こうすると，面外歪みが計算でき，面外応力が0であることが検証できる．左端が肯定され右側が強制的に変位された矩形の鋼板がある．領域，変数，パラメータを設定する．変数には3方向すべてが含まれている：

Wolfram Language code:

Ω = Rectangle[{0, 0}, {40 * 10 ^ -3, 30 * 10 ^ -3}];
vars = {{u[x, y], v[x, y], w[x, y]}, {x, y, z}};
pars = <|"SolidMechanicsModelForm" -> "ExtendedPlaneStress", "YoungModulus" -> 200 * 10 ^ 9, "PoissonRatio" -> 0.3, "Thickness" -> 10 ^ -4|>;

3つの準従属変数で方程式を解く：

Wolfram Language code:

displacement = NDSolveValue[{SolidMechanicsPDEComponent[vars, pars] == {0, 0}, SolidDisplacementCondition[x == 0, vars, pars, <|"Displacement" -> {0, 0}|>], SolidDisplacementCondition[x == 40 * 10 ^ -3, vars, pars, <|"Displacement" -> {-40 / 10 ^ 6, 0}|>]}, {u[x, y], v[x, y], w[x, y]}, {x, y}∈Ω]

変位のリストには3つの出力変数が含まれるようになった．主変数についての変位を可視化する：

Wolfram Language code: VectorDisplacementPlot[displacement[[1 ;; 2]], {x, y}∈Ω, Rule[...]]

歪みを計算する：

Wolfram Language code: strain = SolidMechanicsStrain[vars, pars, displacement]

歪みは3×3配列である．面外歪みを可視化する：

Wolfram Language code: ContourPlot[strain[[3, 3]], {x, y}∈Ω, PlotRange -> All, PlotLegends -> Automatic]

歪みからの応力を計算する：

Wolfram Language code: stress = SolidMechanicsStress[vars, pars, strain]

応力は3×3配列である．平面応力条件を検証する：

Wolfram Language code: stress[[3, 3]]

定常平面歪み解析 (1)

平面歪みのケースを拡張モデルとして計算する．こうすることで，面外応力が計算でき，面外歪みが0であることが検証できる．領域，変数，パラメータを設定する．変数には3方向すべてが含まれる：

Wolfram Language code:

Ω = Rectangle[];
pars = <|"SolidMechanicsModelForm" -> "ExtendedPlaneStrain", "YoungModulus" -> 30 * 10 ^ 3, "PoissonRatio" -> 3 / 10, "Thickness" -> 1|>;
vars = {{u[x, y], v[x, y], 0}, {x, y, z}};

固体力学PDE成分を設定する：

Wolfram Language code: op = SolidMechanicsPDEComponent[vars, pars]

PDEを設定する：

Wolfram Language code:

pde = {op == {0, 0}, SolidFixedCondition[x == 0, vars, pars], SolidDisplacementCondition[x == 1, vars, pars, <|"Displacement" -> {0.1, None}|>]};

PDEを解く：

Wolfram Language code: displacement = NDSolveValue[pde, {u[x, y], v[x, y], 0}, {x, y}∈Ω]

変位による歪みを計算する：

Wolfram Language code: strain = SolidMechanicsStrain[vars, pars, displacement]

歪みは3×3配列である．平面歪み条件を検証する：

Wolfram Language code: strain[[3, 3]]

歪みからの応力を計算する：

Wolfram Language code: stress = SolidMechanicsStress[vars, pars, strain]

応力は3×3配列である．面外応力を可視化する：

Wolfram Language code: ContourPlot[stress[[3, 3]], {x, y}∈Ω, PlotRange -> All, PlotLegends -> Automatic]

定常超弾性平面応力分析 (1)

左側が固定され右側に力が加えられた矩形のゴム板の変位を計算する．領域，変数，パラメータを設定する：

Wolfram Language code:

Ω = Rectangle[{0, 0}, {1, 1}];
vars = {{u[x, y], v[x, y]}, {x, y}};
pars = <|"SolidMechanicsMaterialModel" -> "NeoHookeanIsotropic", "LameParameter" -> 10 ^ 6, "ShearModulus" -> 5000, "SolidMechanicsModelForm" -> "PlaneStress", "Thickness" -> 0.01|>;

方程式を解く：

Wolfram Language code:

displacement = NDSolveValue[
	{SolidMechanicsPDEComponent[vars, pars] == SolidBoundaryLoadValue[x == 1, vars, pars, <|"Force" -> {Quantity[300, "Newtons"], 0}|>], SolidFixedCondition[x == 0, vars, pars]}, {u[x, y], v[x, y]}, {x, y}∈Ω];

変位を可視化する：

Wolfram Language code: VectorDisplacementPlot[displacement, {x, y}∈Rectangle[{0, 0}, {1, 1}], ...]

変位による歪みを計算する：

Wolfram Language code: strains = SolidMechanicsStrain[vars, pars, displacement]

歪みと変位による応力を計算する：

Wolfram Language code: stresses = SolidMechanicsStress[vars, pars, strains, displacement]

歪みを可視化する：

Wolfram Language code: ContourPlot[stresses[[1, 1]], {x, y}∈Ω, PlotRange -> All]

出力応力 (1)

計算されるデフォルトの応力はコーシー(Cauchy)応力である．代りにキルヒホフ(Kirchhoff)応力を計算する：

Wolfram Language code:

vars = {{u[x, y], v[x, y]}, {x, y}};
pars = <|"SolidMechanicsMaterialModel" -> "NeoHookeanIsotropic", "LameParameter" -> 10, "ShearModulus" -> 5, "Thickness" -> 1|>;
displacement = NDSolveValue[{SolidMechanicsPDEComponent[vars, pars] == SolidBoundaryLoadValue[x == 1, vars, pars, <|"Force" -> {10, 0}|>], SolidFixedCondition[x == 0, vars, pars]}, {u[x, y], v[x, y]}, {x, y}∈Rectangle[{0, 0}, {1, 1}]]

歪みを計算する：

Wolfram Language code: strain = SolidMechanicsStrain[vars, pars, displacement]

キルヒホフ応力を計算する：

Wolfram Language code: SolidMechanicsStress[vars, Join[pars, <|"OutputStressMeasure" -> "Kirchhoff"|>], strain, displacement]

考えられる問題 (1)

軸対称の場合は，転移が空間座標の関数であることが重要である．その理由を説明するために，変数，パラメータ，空間の関数ではない転移関数を作成する：

Wolfram Language code:

vars = {{u[r, z], w[r, z]}, {r, z}};
pars = <|"RegionSymmetry" -> "Axisymmetric", "YoungModulus" -> 1, "PoissonRatio" -> 1 / 3|>;
usol = wsol = FunctionInterpolation[0, {r, 0, 1}, {z, 0, 1}]

生成されたInterpolatingFunctionは空間座標およびの関数ではない点に注意のこと．この状態で歪みと応力を計算すると，応力テンソルにやはり空間座標を持たない何らかの補間関数が現れる：

Wolfram Language code:

strain = SolidMechanicsStrain[vars, pars, {usol, wsol}];
SolidMechanicsStress[vars, pars, strain, {usol, wsol}][[1, 1]]

これは，軸対称の場合の式では，歪みの成分がとして計算されるためである．ここで，は最初の従属変数，は円筒座標系の半径方向である．導出は軸対称モデルのセクションで説明されている．歪みから応力が計算されるとき，の値は最初に指定された変位関数 (この場合は usol) から取得される．その関数が独立変数とに依存しない場合，それらは出力に表示されない．

これを避けるためには，変位に空間座標とを使う必要がある：

Wolfram Language code: usol = wsol = FunctionInterpolation[0, {r, 0, 1}, {z, 0, 1}][r, z]

これで，応力テンソルのすべてのInterpolatingFunction成分が空間座標を利用するようになった：

Wolfram Language code:

strain = SolidMechanicsStrain[vars, pars, {usol, wsol}];
SolidMechanicsStress[vars, pars, strain, {usol, wsol}][[1, 1]]

Top

その他のラーニングリソース

テクニカルサポート

データサイエンス，金融，ビジネス

工学

科学とテクノロジー

教育のためのテクノロジー

教育イニシアチブ

使い始める

Grow Your Skills

Wolframと繋がる

大人用の教育プログラム

若者のための教育プログラム

読む

SolidMechanicsStress

詳細

例題

例 (1)

スコープ (5)

定常解析 (1)

定常平面応力解析 (1)

定常平面歪み解析 (1)

定常超弾性平面応力分析 (1)

出力応力 (1)

考えられる問題 (1)

テキスト

CMS

APA

BibTeX

BibLaTeX

SolidMechanicsStress

詳細

例題

例 (1)

スコープ (5)

定常解析 (1)

定常平面応力解析 (1)

定常平面歪み解析 (1)

定常超弾性平面応力分析 (1)

出力応力 (1)

考えられる問題 (1)

関連項目

テクニカルノート

関連するガイド

履歴

テキスト

CMS

APA

BibTeX

BibLaTeX