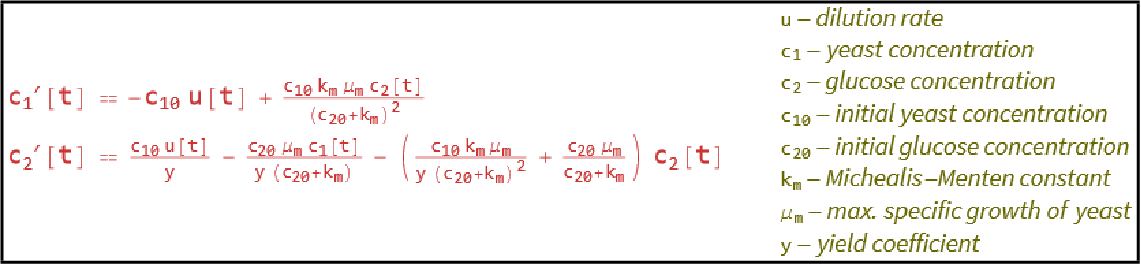StateSpaceModel
StateSpaceModel[{a,b,c,d}]
表示状态矩阵为 a、输入矩阵为 b、输出矩阵为 c 和传输矩阵为 d 的状态空间模型.
StateSpaceModel[{a,b,c,d,e}]
表示具有描述符矩阵 e 的描述符状态空间模型.
StateSpaceModel[sys]
给出对应于系统模型 sys 的状态空间模型.
StateSpaceModel[eqns,{{x1,x10},…},{{u1,u10},…},{g1,…},τ]
给出通过输出为 y、自变量为 τ 的常微分或者差分方程 eqns 关于点 (xi 0,ui 0) 的泰勒线性化而取得的状态空间模型.
更多信息和选项


- StateSpaceModel 亦称为 LTI 系统(线性时不变).
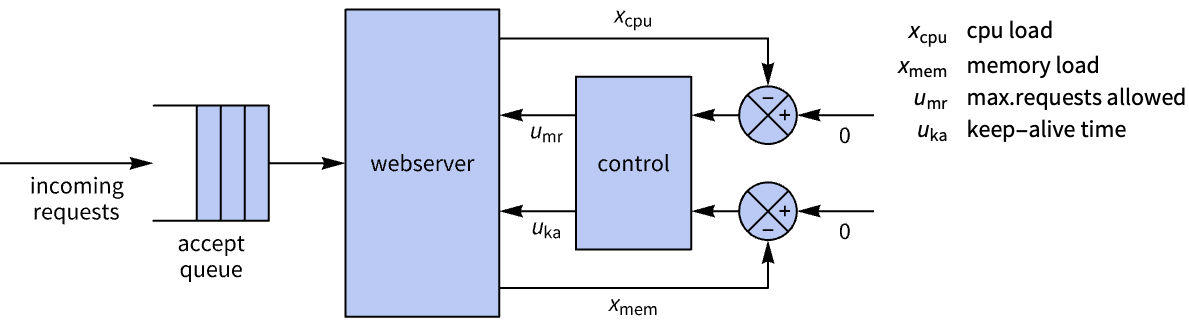
- StateSpaceModel 通常用作控制器设计系统的线性化模型.
- 由方程
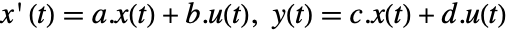 建模,并且具有状态
建模,并且具有状态 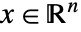 、控制输入
、控制输入 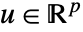 和输出
和输出 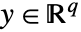 的连续时间系统可以指定为 StateSpaceModel[{a,b,c,d}].
的连续时间系统可以指定为 StateSpaceModel[{a,b,c,d}]. - 由方程
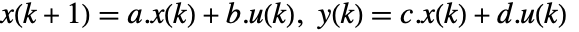 建模,并且具有状态
建模,并且具有状态 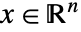 、控制输入
、控制输入 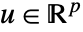 、输出
、输出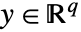 和采样周期 τ 的离散时间系统可以指定为 StateSpaceModel[{a,b,c,d},SamplingPeriod->τ].
和采样周期 τ 的离散时间系统可以指定为 StateSpaceModel[{a,b,c,d},SamplingPeriod->τ]. - 可用以下形式指定描述符系统:
-
StateSpaceModel[{a,b,c,d,e}] 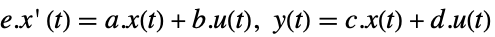
StateSpaceModel[{a,b,c,d,e},SamplingPeriod->τ] 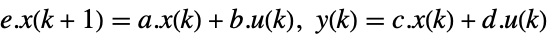
- 可通过在任何矩阵中使用 SystemsModelDelay 来表示时延系统.
- 对于具有 n 个状态、p 个输入和 q 个输出的系统,矩阵 a、b、c、d 和 e 应该具有维度 {n,n}、{n,p}、{q,n}、{q,p} 和 {n,n}.
- 可以使用下列简短输入:
-
StateSpaceModel[{a,b,c}] 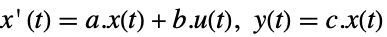
StateSpaceModel[{a,b}] 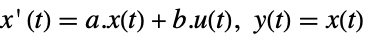
StateSpaceModel[{a,b,c,Automatic,e}] 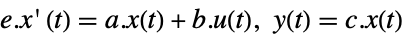
StateSpaceModel[{a,b,Automatic,Automatic,e}] 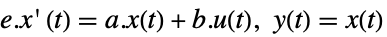
- 在 StateSpaceModel[sys] 中如下系统可被转换:
-
AffineStateSpaceModel 近似泰勒转化 NonlinearStateSpaceModel 近似泰勒转化 TransferFunctionModel 精确转化 - 当从传递函数模型 sys 进行转化时,使用可控制实现.
- 对于方程式输入,默认的线性化点 xi0 和 uj0 为零.
- 可以给出下列选项:
-
DescriptorStateSpace Automatic 标准或者描述器实现 ExternalTypeSignature Automatic 嵌入代码的变量类型 SamplingPeriod None 采样周期 StateSpaceRealization Automatic 规范实现 SystemsModelLabels None 输入、输出和状态变量的标签
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (34)
基本用途 (12)
可在 AffineStateSpaceModel 表示中看到这些变量:
描述符模型 (6)
用 Automatic 创建一个描述符系统,将所有状态作为输出:
时延模型 (3)
模型转换 (13)
选项 (14)
StateSpaceRealization (4)
应用 (33)
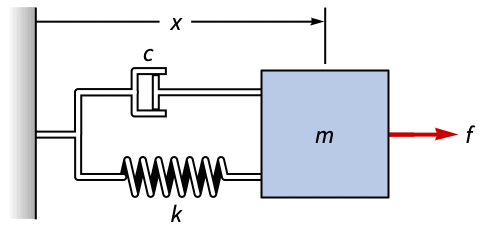
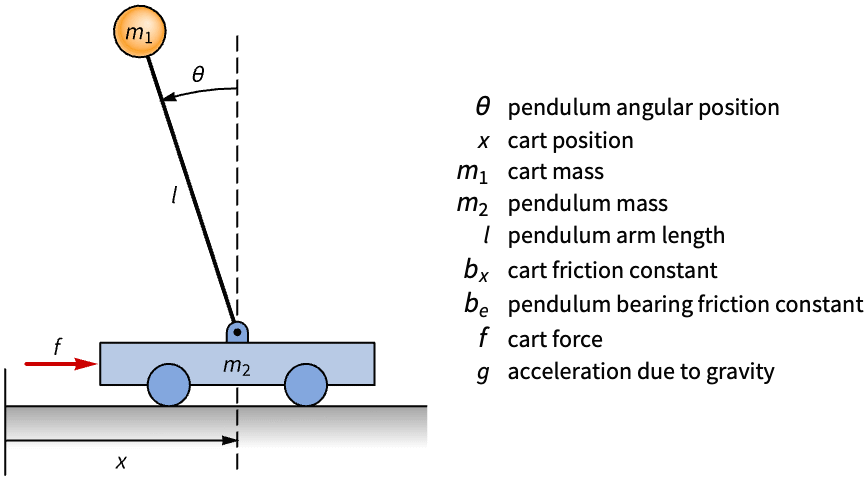
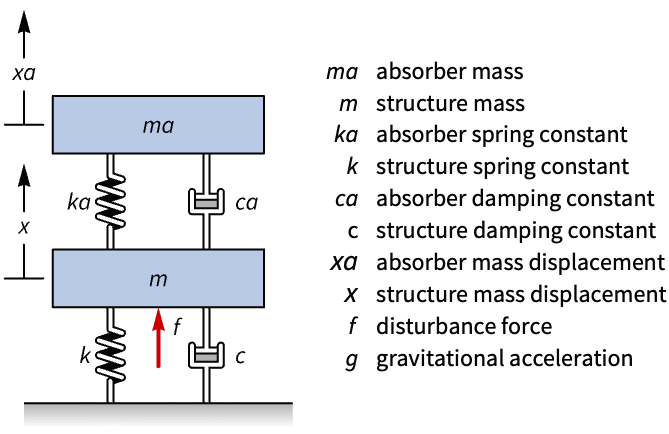
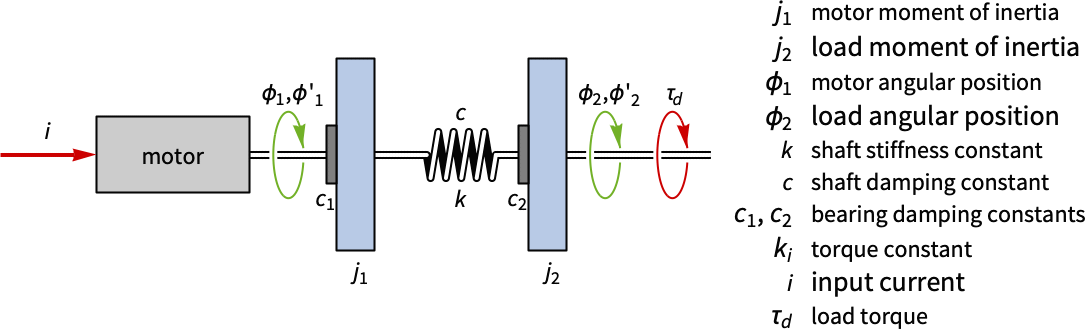
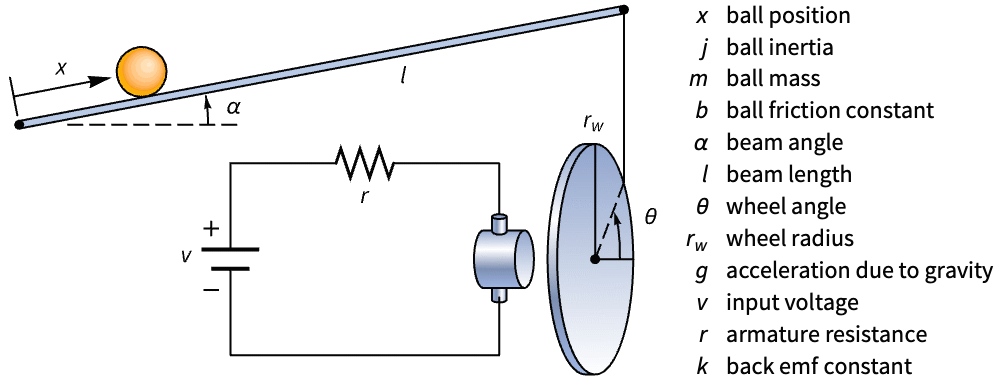
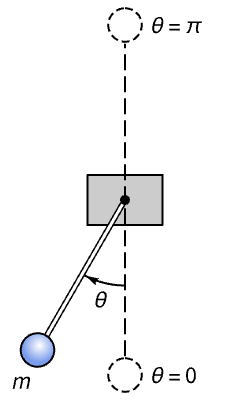
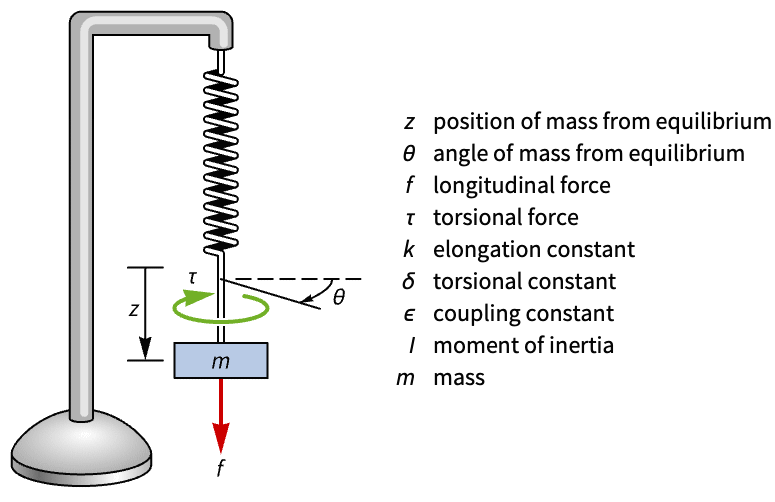
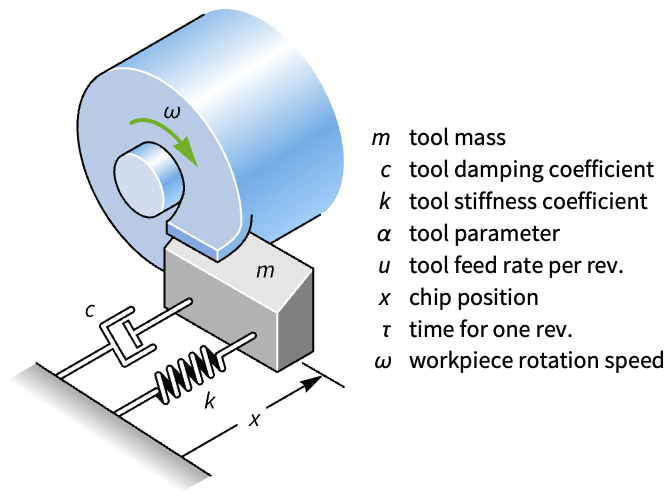
机械系统 (11)
航空航天系统 (6)
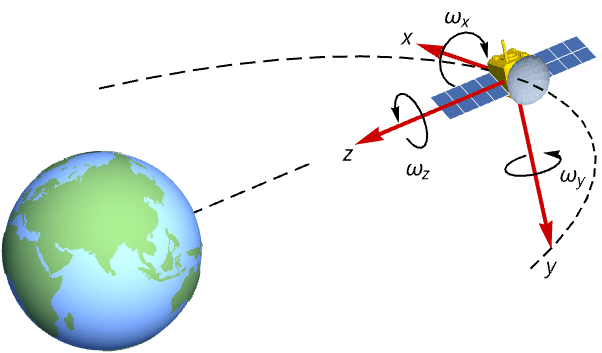
状态空间模型在航空航天系统建模中非常有用. 根据欧拉运动方程开始构建卫星姿态动力学的状态空间模型:
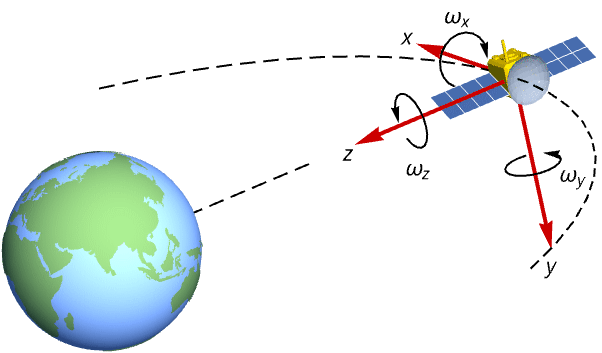
状态空间模型可用于模型分析. 构建 Harrier VTOL 喷气式飞机的状态空间模型并评估其可控性:
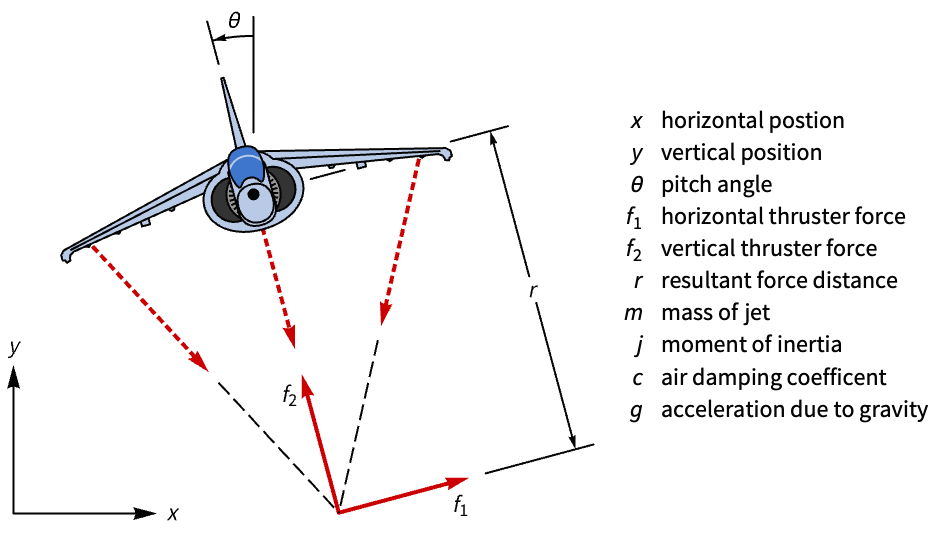
状态空间模型对于分析 MIMO 系统非常有用,其中多个输入会影响给定的输出. 使用状态空间模型表示比较副翼和方向舵对使用状态反馈控制的波音 747 偏航动力学的有效性:
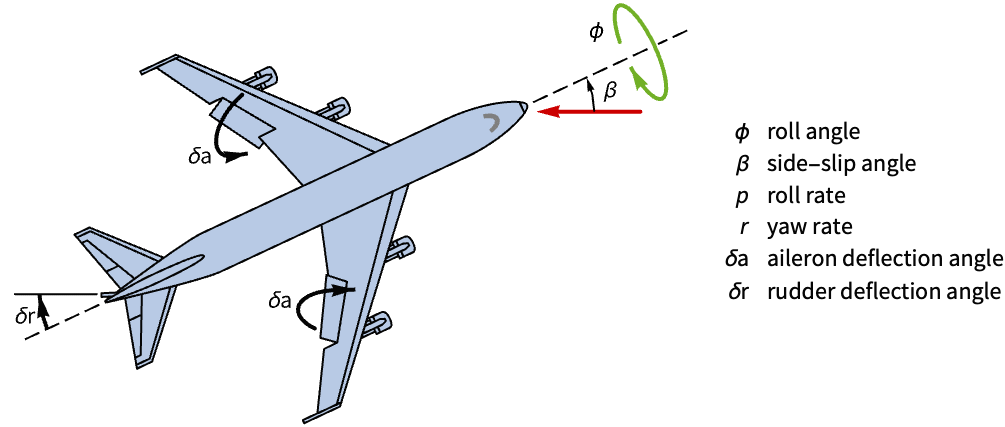
根据一组状态、输入和输出矩阵构建的飞机横向运动的状态空间模型:
状态空间模型对于离散时间状态反馈控制器的设计非常有用. 获取 747 纵向动力学的状态空间模型,并使用离散时间状态反馈控制改善其操纵性能:
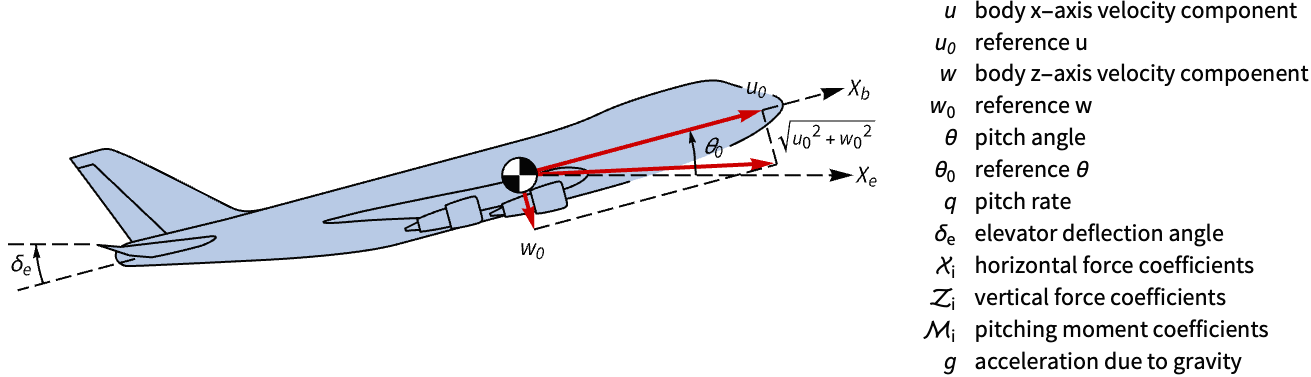
离散时间控制器也可以通过对连续时间模型进行近似来设计. 通过对连续时间状态空间模型进行近似来设计离散时间控制器以稳定 Harrier VTOL 喷气式飞机: »
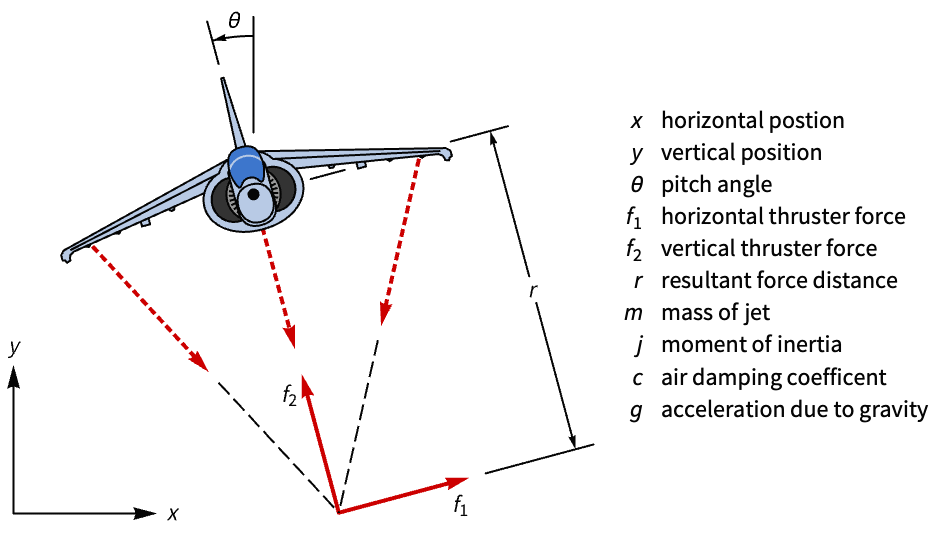
如果没有控制器,当喷气机的俯仰角受到干扰时,其水平位置将不受控制:
状态空间模型还可用于设计输出反馈控制器,如估计调节器. 用离散时间模型设计一个估计调节器,跟踪卫星维持天底指向方向所需的角速率: »
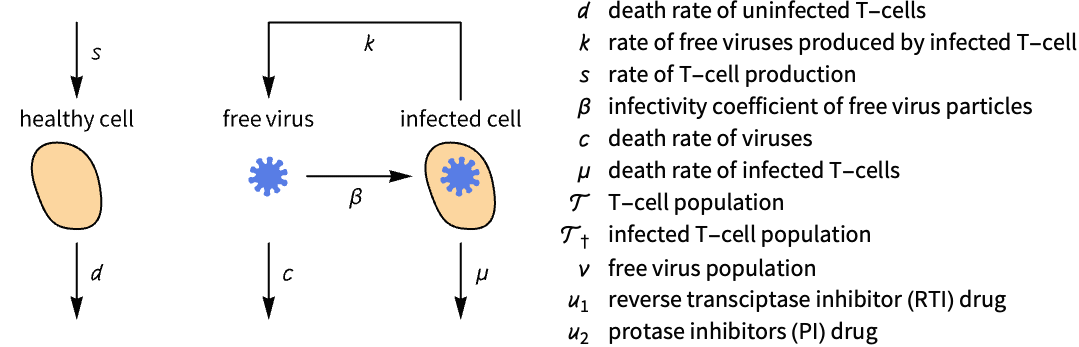
生物系统 (2)
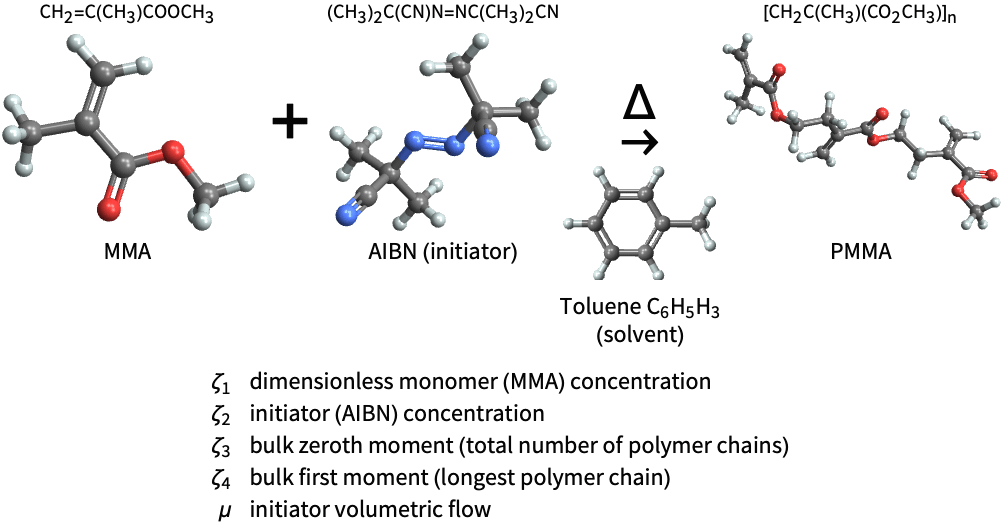
化学系统 (3)
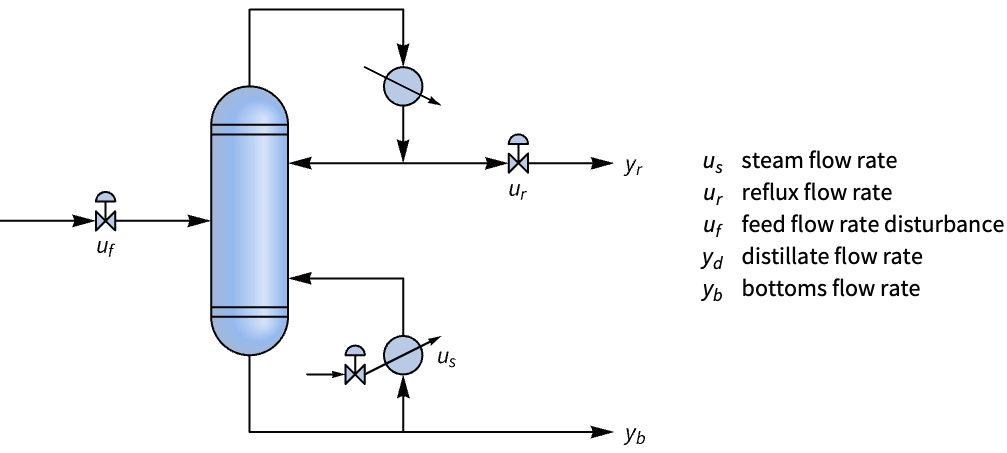
电子系统 (4)
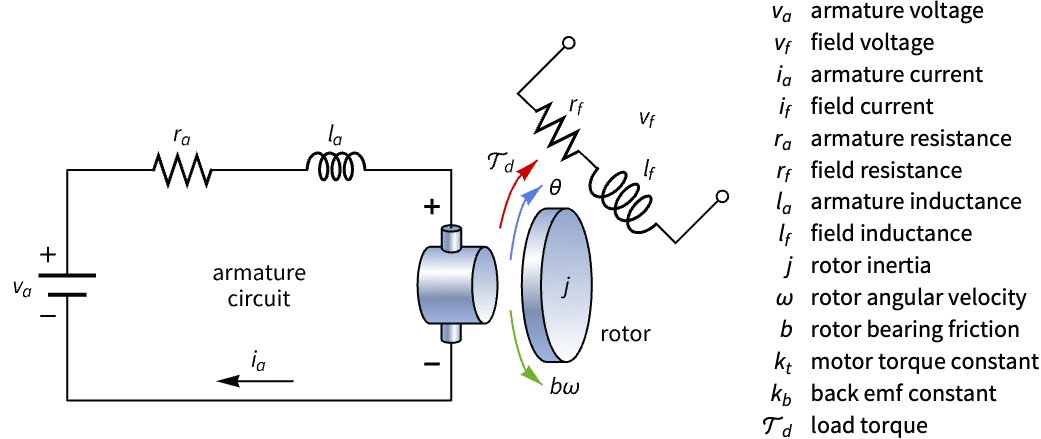
构建具有电枢和励磁电压输入的直流电机的状态空间模型,并分析其可控性:
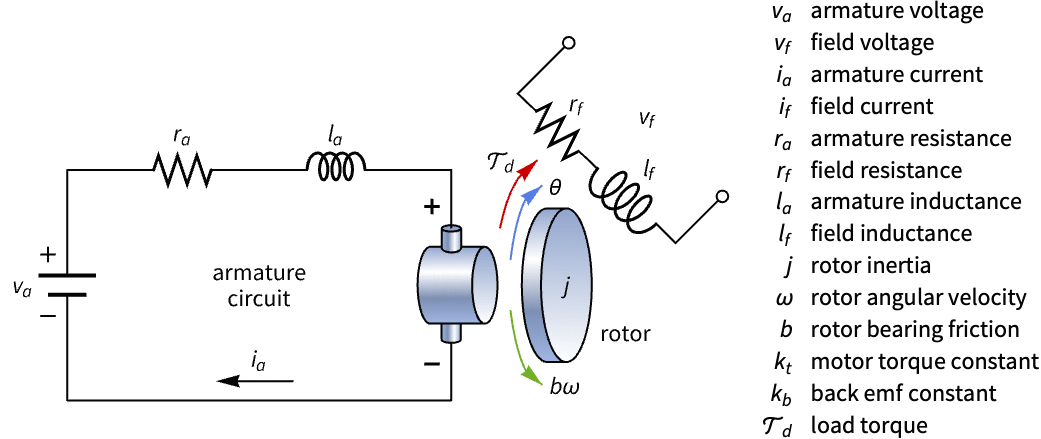
符号状态空间模型可用于模拟具有参数的模型. 根据运算放大器 (op amp) 电路的控制方程构建其符号状态空间模型,并分析其在不同参数值下的输出相位和幅度:
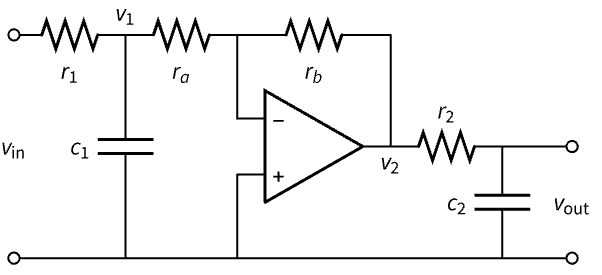
状态空间模型可以表示微分和代数方程混合的系统. 根据 RLC 电路的微分方程构建其描述符状态空间模型,根据 RLC 电路的微分方程构建其标准状态空间模型:
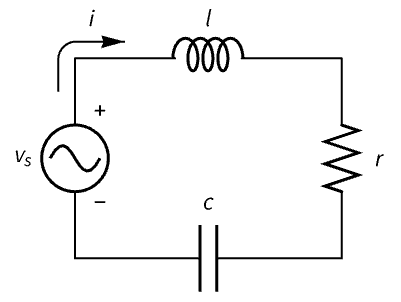
由于 Kirchhoff 方程是代数方程,因此得到的是描述状态空间模型:
状态空间模型可用于解决跟踪问题. 在变化的扭矩负载和有传感器噪声的情况下,为直流电机设计基于估计器的跟踪控制器: »
信息系统 (1)
随机过程 (6)
文本
Wolfram Research (2010),StateSpaceModel,Wolfram 语言函数,https://reference.wolfram.com/language/ref/StateSpaceModel.html (更新于 2014 年).
CMS
Wolfram 语言. 2010. "StateSpaceModel." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/StateSpaceModel.html.
APA
Wolfram 语言. (2010). StateSpaceModel. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/StateSpaceModel.html 年