SymmetricMatrix[smat]
converts the symmetric matrix smat to a structured array.


SymmetricMatrix
SymmetricMatrix[smat]
converts the symmetric matrix smat to a structured array.
Details and Options


- Symmetric matrices, when represented as structured arrays, allow for a convenient specification.
- Symmetric matrices typically result from Hessian matrices as used in optimization or covariance, from correlation matrices in statistics and matrix representations of quadratic forms or undirected graphs.
- For symmetric matrices, it is significantly less expensive to solve eigenproblems that arise in applications.
- A symmetric matrix
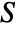 satisfies sij=sji, which means they are symmetric across the diagonal.
satisfies sij=sji, which means they are symmetric across the diagonal. - The elements sij need not be numerical.
- The inverse of a symmetric matrix and, in general, any matrix function of a symmetric matrix is also symmetric.
- For a SymmetricMatrix sa, the following properties "prop" can be accessed as sa["prop"]:
-
"Matrix" symmetric matrix, represented as a full array "Properties" list of supported properties "Structure" type of structured array "StructuredData" internal data stored by the structured array "StructuredAlgorithms" list of functions with special methods for the structured array "Summary" summary information, represented as a Dataset - Normal[SymmetricMatrix[…]] gives the symmetric matrix as an ordinary matrix.
- SymmetricMatrix[…,TargetStructure->struct] returns the symmetric matrix in the format specified by struct. Possible settings include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense matrix "Structured" represent the matrix as a structured array - SymmetricMatrix[…,TargetStructureAutomatic] is equivalent to SymmetricMatrix[…,TargetStructure"Structured"].

Examples
open all close allBasic Examples (1)
Normal can convert a SymmetricMatrix to its ordinary representation:
Scope (5)
Construct a symmetric matrix from its upper-triangular entries:
The matrix can also be constructed from its lower-triangular entries:
The Hilbert matrix is a symmetric matrix:
Real reflection matrices are both symmetric and orthogonal:
The matrix is symmetric, but not Hermitian:
SymmetricMatrix objects include properties that give information about the matrix:
The "Summary" property gives a brief summary of information about the matrix:
The "StructuredAlgorithms" property lists the functions that have structured algorithms:
Options (1)
Applications (8)
The Hessian matrix of a multivariate function with continuous second partial derivatives is symmetric (Schwarz's theorem):
Covariance and correlation matrices are symmetric:
Symmetric matrices can be obtained from quadratic forms:
Adjacency matrices of undirected graphs are sparse and symmetric:
Matrices drawn from GaussianOrthogonalMatrixDistribution are symmetric:
Matrices drawn from CircularOrthogonalMatrixDistribution are symmetric and unitary:
A symmetric positive-definite matrix ![]() can be used to define an inner product by
can be used to define an inner product by ![]() :
:
Verify that ![]() is positive definite:
is positive definite:
Orthogonalize the standard basis of ![]() to find an orthonormal basis:
to find an orthonormal basis:
Confirm that this basis is orthonormal with respect to the inner product ![]() :
:
The moment of inertia tensor is the equivalent of mass for rotational motion. For example, kinetic energy is ![]() , with
, with ![]() taking the place of the mass
taking the place of the mass ![]() and angular velocity
and angular velocity ![]() taking the place of linear velocity
taking the place of linear velocity ![]() in the formula
in the formula ![]() .
. ![]() can be represented by a positive-definite symmetric matrix. Compute the moment of inertia for a tetrahedron with endpoints at the origin and positive coordinate axes:
can be represented by a positive-definite symmetric matrix. Compute the moment of inertia for a tetrahedron with endpoints at the origin and positive coordinate axes:
Compute the kinetic energy if its angular velocity is ![]() :
:
The kinetic energy is positive as long as ![]() is nonzero, showing the matrix was positive definite:
is nonzero, showing the matrix was positive definite:
Properties & Relations (4)
The transpose of a symmetric matrix equals the original matrix:
A symmetric matrix has symmetry Symmetric[{1,2}]:
A symmetric matrix can be represented using SymmetrizedArray or SymmetricMatrix:
The two representations are equal, but support different algorithms:
SymmetrizedArray supports tensorial operations such as D, Flatten, Inner and Outer:
SymmetricMatrix supports matrix-specific operations such as KroneckerProduct:
A real symmetric matrix can also be represented using HermitianMatrix:
This is not true of a complex symmetric matrix:

Related Guides
History
Text
Wolfram Research (2024), SymmetricMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/SymmetricMatrix.html.
CMS
Wolfram Language. 2024. "SymmetricMatrix." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SymmetricMatrix.html.
APA
Wolfram Language. (2024). SymmetricMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SymmetricMatrix.html
BibTeX
@misc{reference.wolfram_2025_symmetricmatrix, author="Wolfram Research", title="{SymmetricMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/SymmetricMatrix.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_symmetricmatrix, organization={Wolfram Research}, title={SymmetricMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/SymmetricMatrix.html}, note=[Accessed: 25-February-2026]}